José R. Correa, Laurent Feuilloley, José A. Soto.
LATIN 2014: Theoretical Informatics - 11th Latin American Symposium, Montevideo, Uruguay, March 31 - April 4, 2014
doi:10.1007/978-3-642-54423-1_4
Abstract
Finding a maximum independent set of a given family of axis-parallel rectangles is a basic problem in computational geometry and combinatorics. This problem has attracted significant attention since the sixties, when Wegner conjectured that the corresponding duality gap, i.e., the maximum possible ratio between the maximum independent set and the minimum hitting set, is bounded by a universal constant.
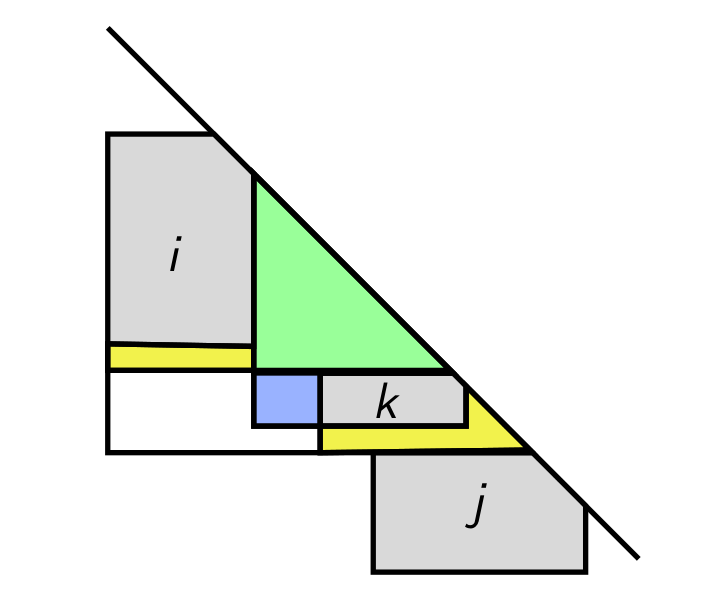
In this paper we improve upon recent results of Chepoi and Felsner and prove that when the given family of rectangles is intersected by a diagonal, this ratio is between 2 and 4. For the upper bound we derive a simple combinatorial argument that first allows us to reprove results of Hixon, and Chepoi and Felsner and then we adapt this idea to obtain the improved bound in the diagonal intersecting case.
From a computational complexity perspective, although for general rectangle families the problem is known to be NP-hard, we derive an $O(n^2)$-time algorithm for the maximum weight independent set when, in addition to intersecting a diagonal, the rectangles intersect below it. This improves and extends a classic result of Lubiw. As a consequence, we obtain a 2-approximation algorithm for the maximum weight independent set of rectangles intersecting a diagonal.