Multigrid Convergent Principal Curvature Estimators in Digital Geometry

David Coeurjolly, Jacques-Olivier Lachaud, Jérémy Levallois

Computer Vision and Image Understanding June 2014

Abstract

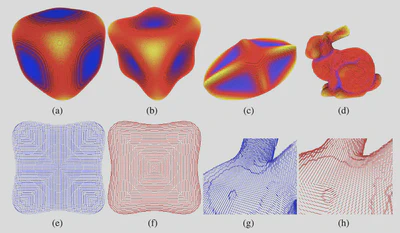
In many geometry processing applications, the estimation of differential geometric quantities such as curvature or normal vector field is an essential step. In this paper, we investigate a new class of estimators on digital shape boundaries based on integral invariants (Pottmann et al., 2007) [39]. More precisely, we provide both proofs of multigrid convergence of principal curvature estimators and a complete experimental evaluation of their performances.

Type

Journal article

Publication

Computer Vision and Image Understanding

Caption: * Illustration of 3D curvature estimation. Mean curvature on rounded cube (a), Goursat’s surface (b), Leopold surface (c) and a bunny (d). First principal direction and second principal direction Goursat’s surface (e and f) and Stanford bunny (g and h).*

@article{dcoeurjo_Levallois_CVIU14,
      author = {David Coeurjolly and Jacques-Olivier Lachaud and Jérémy Levallois},
      journal = {Computer Vision and Image Understanding},
      language = {en},
      month = {June},
      number = {1},
      pages = {27-41},
      publisher = {Elsevier},
      title = {Multigrid Convergent Principal Curvature Estimators in Digital Geometry},
      url = {http://liris.cnrs.fr/publis/?id=6625},
      volume = {129},
      year = {2014}
}