Sobol’ Sequences with Guaranteed-Quality 2D Projections

Abstract

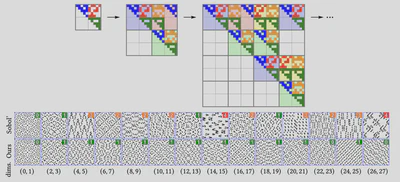
Low-discrepancy sequences, and more particularly Sobol’ sequences are gold standard for drawing highly uniform samples for quasi-Monte Carlo applications. They produce so-called (𝑡,𝑠)-sequences, that is, sequences of 𝑠-dimensional samples whose uniformity is controlled by a non-negative integer quality factor 𝑡. The Monte Carlo integral estimator has a convergence rate that improves as 𝑡 decreases. Sobol’ construction in base 2 also provides extremely fast sampling point generation using efficient xor-based arithmetic. Computer graphics applications, such as rendering, often require high uniformity in consecutive 2D projections and in higher-dimensional projections at the same time. However, it can be shown that, in the classical Sobol’ construction, only a single 2D sequence of points (up to scrambling), constructed using irreducible polynomials 𝑥 and 𝑥+1, achieves the ideal 𝑡 = 0 property. Reusing this sequence in projections necessarily loses high dimensional uniformity. We prove the existence and construct many 2D Sobol’ sequences having 𝑡 = 1 using irreducible polynomials 𝑝 and 𝑝^2 +𝑝+1. They can be readily combined to produce higher-dimensional low discrepancy sequences with a high-quality 𝑡 = 1, guaranteed in consecutive pairs of dimensions. We provide the initialization table that can be directly used with any existing Sobol’ implementation, along with the corresponding generator matrices, for an optimized 692-dimensional Sobol’ construction. In addition to guaranteeing the (1,2)-sequence property for all consecutive pairs, we ensure that 𝑡 ≤4 for consecutive 4D projections up to 215 points.

We demonstrate that 2D Sobol’ sequences constructed with polynomials 𝑝and 𝑝2 +𝑝+1 have a characteristic matrix 𝐾= 𝑀𝑝2+𝑝+1𝑀−1 𝑝 that can be obtained with a simple recursive algorithm. This is illustrated using polynomials of degrees 𝑒 = 5 and 2𝑒 = 10, where each colored block has dimensions 𝑒×𝑒. They produce high-quality (1,2)-sequences (with quality factor 𝑡 = 1) under mild conditions on 𝐾’s blocks and 𝑝(bottom). The quality factor 𝑡 of each point set is indicated in the upper-right corner of each patch (only 256 points are shown). We use these (1,2)-sequences to construct higher-dimensional low-discrepancy sequences with high-quality 2D and 4D projections.