Cubic curves. More...

#include <curve.h>

Public Member Functions
	CubicCurve ()
	Empty.

	CubicCurve (const Cubic &, const Cubic &, const Cubic &)
	Creates a cubic curve. More...

	~CubicCurve ()
	Empty.

Cubic &	operator[] (int)
	Access curve components.

Cubic	operator[] (int) const
	Access curve components.

CubicCurve	operator+ () const
	Overloaded out of consistency.

CubicCurve	operator- () const
	Negative curve unary operator.

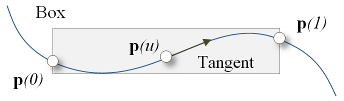
QuadricCurve	Tangent () const
	Computes the quadric curve whose components are defined as the derivative of the cubic coordinates of the curve. More...

Vector	Tangent (const double &) const
	Computes the tangent to the cubic curve at a given position on the curve. More...

Vector	Normal (const double &) const
	Computes the normal vector to the cubic curve at a given position on the curve. More...

double	Curvature (const double &) const
	Computes the 3D curvature to the curve at t. More...

double	S (const double &, int=256) const
	Compute the curvilign absisca of a point on the curve. More...

double	U (const double &, int=256) const
	Compute the parameter corresponding to the argument curvilign absisca of a point on the curve. More...

double	Length (int=256) const
	Computes the length of the cubic curve. Integration is performed over interval [0,1]. More...

double	Length (const double &, const double &, int=256) const
	Computes the length of the cubic curve over interval [a,b]. More...

double	InverseArcLength (const double &, int=256) const
	Compute the parameter t corresponding to a given input arc length. More...

Vector	operator() (const double &) const
	Evaluates curve point at a given location. More...

Vector	Eval (const double &) const
	Evaluates curve point at a given location. More...

Box	GetBox () const
	Compute the bounding box of the cubic curve with parameter interval [0,1]. More...

double	R (const Vector &, double &) const
	Returns the squared distance between a point and the cubic curve. More...

Matrix	GetMatrix (const double &) const
	Compute the Frenet vectors at a given point on the curve. More...

Frame	GetFrame (const double &) const
	Compute the Frenet frame at a given point on the curve. More...

Vector	BezierControl (int) const
	Compute the i-th B�zier control point of the curve. More...

void	Approximate (QuadricCurve &, QuadricCurve &, const double &=0.5) const
	Approximate a cubic curve by two quadric curves. More...

Static Public Member Functions
static CubicCurve	Hermite (const Vector &, const Vector &, const Vector &, const Vector &)
	Creates an Hermite cubic curve on interval [0,1] given vertex locations and tangent vectors (in that order). More...

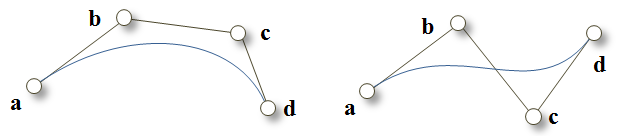
static CubicCurve	Bezier (const Vector &, const Vector &, const Vector &, const Vector &)
	Creates a Bezier cubic curve on interval [0,1] given four vertex locations. More...

Protected Attributes
Cubic	z
	Cubic polynomial functions for every coordinate.

Friends
std::ostream &	operator<< (std::ostream &, const CubicCurve &)
	Overloaded. More...

Detailed Description

Cubic curves.

Cubic curves are implemented with three cubic polynomials defining the coordinates of the points on the curve. It is a minimum storage class in the sense that it does not keep extra constant data which may be useful for computing the bounding box of the quadric curve parameterized over the unit interval [0,1] or the distance between a point an the curve.

Constructor & Destructor Documentation

◆ CubicCurve()

CubicCurve::CubicCurve	(	const Cubic &	x,
		const Cubic &	y,
		const Cubic &	z
	)

Creates a cubic curve.

Parameters

x,y,z Cubic equations of the coordinates.

Member Function Documentation

◆ Approximate()

void CubicCurve::Approximate	(	QuadricCurve &	a,
		QuadricCurve &	b,
		const double &	gamma = `0.5`
	)		const

Approximate a cubic curve by two quadric curves.

N. Truong, C. Yuksel and L. Seiler. Quadratic Approximation of Cubic Curves. Proceedings of the ACM on Computer Graphics and Interactive Techniques. 2020.

Parameters

gamma	Subdision parameter, in [0,1].
a,b	Returned quadric curves.

◆ Bezier()

CubicCurve CubicCurve::Bezier	(	const Vector &	a,
		const Vector &	b,
		const Vector &	c,
		const Vector &	d
	)

static

Creates a Bezier cubic curve on interval [0,1] given four vertex locations.

Parameters

a,b,c,d Vertices of the Bezier curve.

◆ BezierControl()

Vector CubicCurve::BezierControl ( int i ) const

inline

Compute the i-th B�zier control point of the curve.

Computations have been optimized.

Parameters

i Index.

◆ Curvature()

double CubicCurve::Curvature ( const double & t ) const

Computes the 3D curvature to the curve at t.

Parameters

t	Parameter.

◆ Eval()

Vector CubicCurve::Eval ( const double & t ) const

Evaluates curve point at a given location.

Parameters

t	Parameter.

◆ GetBox()

Box CubicCurve::GetBox ( ) const

Compute the bounding box of the cubic curve with parameter interval [0,1].

This function is computationnally intensive as the bounds are found by evaluating the range of every coordinate within [0,1].

◆ GetFrame()

Frame CubicCurve::GetFrame ( const double & u ) const

Compute the Frenet frame at a given point on the curve.

Parameters

u	Parameter.

◆ GetMatrix()

Matrix CubicCurve::GetMatrix ( const double & u ) const

Compute the Frenet vectors at a given point on the curve.

The columns of the returned matrix contain the tangent, binormal and normal vectors.

Parameters

u	Parameter.

◆ Hermite()

CubicCurve CubicCurve::Hermite	(	const Vector &	a,
		const Vector &	b,
		const Vector &	ta,
		const Vector &	tb
	)

static

Creates an Hermite cubic curve on interval [0,1] given vertex locations and tangent vectors (in that order).

Parameters

a,b	End vertices of the Hermite cubic curve.
ta,tb	Tangent vectors at the end vertices.

◆ InverseArcLength()

double CubicCurve::InverseArcLength	(	const double &	s,
		int	n = `256`
	)		const

Compute the parameter t corresponding to a given input arc length.

Parameters

s	Arc length, which should be positive.
n	Discretization of the curve.

◆ Length() [1/2]

double CubicCurve::Length	(	const double &	a,
		const double &	b,
		int	n = `256`
	)		const

Computes the length of the cubic curve over interval [a,b].

Since we have the parametric equations of the coordinates of the points on the curve, then the length is the integral of the square root of the sum of the squared derivatives where the limits of integration are [a,b].

s = Integral Sqrt((dx/dt)² + (dy/dt)²) dt,

In the general case, the function we end up with is not integrable in closed form, leading to an elliptic integral or some such. Thus we evaluate the integral numerically.

Parameters

a,b	Interval.
n	Discretization of the integration interval.

◆ Length() [2/2]

double CubicCurve::Length ( int n = 256 ) const

Computes the length of the cubic curve. Integration is performed over interval [0,1].

This function simply calls CubicCurve::Length(0.0,1.0,n) with n as the passed argument parameter.

Parameters

n	Discretization of the curve.

◆ Normal()

Vector CubicCurve::Normal ( const double & t ) const

Computes the normal vector to the cubic curve at a given position on the curve.

The normal is the obtained by evaluating the second derivative.

Parameters

t Position.

◆ operator()()

Vector CubicCurve::operator() ( const double & t ) const

Evaluates curve point at a given location.

Parameters

t	Parameter.

◆ R()

double CubicCurve::R	(	const Vector &	p,
		double &	u
	)		const

Returns the squared distance between a point and the cubic curve.

This function computes the projection of a point p onto the curve by minimizing the distance function along the curve, expressed as a degree 5 polynomial.

Most of the coefficients of this polynomial are constant, and could be pre-processed in the constructor.

Note that this function is computationnally intensive, and ~25 times slower than QuadricCurve::R(). Therefore, cubic curves should be used with care as distance queries are called many times.

See also: QuadricCurve::R()

Parameters

p	Point.
u	Parameter defining the coordinate of the projection of the argument vertex onto the curve.

Returns: The distance.

◆ S()

double CubicCurve::S	(	const double &	t,
		int	n = `256`
	)		const

Compute the curvilign absisca of a point on the curve.

Parameters

t	Parameter that should be within [0,1] interval.
n	Discretization of the integration interval.

◆ Tangent() [1/2]

QuadricCurve CubicCurve::Tangent ( ) const

Computes the quadric curve whose components are defined as the derivative of the cubic coordinates of the curve.

This function is useful for preprocessing tangent computations.

◆ Tangent() [2/2]

Vector CubicCurve::Tangent ( const double & t ) const

Computes the tangent to the cubic curve at a given position on the curve.

The tangent is the obtained by evaluating the first derivative.

See also: CubicCurve::Tangent()

Parameters

t Position.

◆ U()

double CubicCurve::U	(	const double &	s,
		int	n = `256`
	)		const

Compute the parameter corresponding to the argument curvilign absisca of a point on the curve.

Parameters

s	Argument curvilign absisca (should be between 0.0 and the length of the curve).
n	Discretization of the integration interval.

Friends And Related Function Documentation

◆ operator<<

std::ostream & operator<<	(	std::ostream &	s,
		const CubicCurve &	curve
	)

friend

Overloaded.

Parameters

s	Stream.
curve	The cubic curve.

Public Member Functions

Static Public Member Functions

Protected Attributes

Friends

Detailed Description

Constructor & Destructor Documentation

◆ CubicCurve()

Member Function Documentation

◆ Approximate()

◆ Bezier()

◆ BezierControl()

◆ Curvature()

◆ Eval()

◆ GetBox()

◆ GetFrame()

◆ GetMatrix()

◆ Hermite()

◆ InverseArcLength()

◆ Length() [1/2]

◆ Length() [2/2]

◆ Normal()

◆ operator()()

◆ R()

◆ S()

◆ Tangent() [1/2]

◆ Tangent() [2/2]

◆ U()

Friends And Related Function Documentation

◆ operator<<