PODC 2015: 34th Annual ACM Symposium on Principles of Distributed Computing, Donostia-San Sebastián, Spain, July 2015
doi:10.1145/2767386.2767446
Abstract
A standard model in network synchronised distributed computing is the LOCAL model. In this model, the processors work in rounds and, in the classic setting, they know the number of vertices of the network, n. Using n, they can compute the number of rounds after which they must all stop and output.
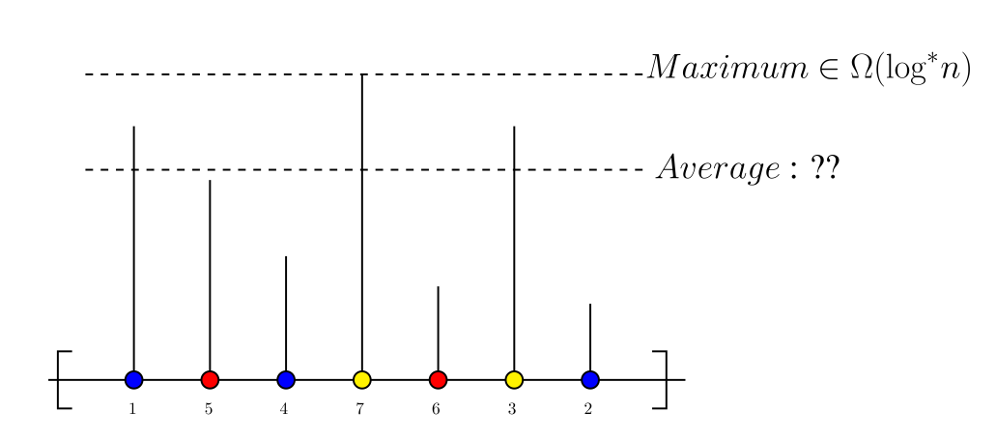
It has been shown recently that for many problems, one can basically remove the assumption about the knowledge of n, without increasing the asymptotic running time. In this case, it is assumed that different vertices can choose their final output at different rounds, but continue to transmit messages. In both models, the measure of the running time is the number of rounds before the last node outputs.
In this brief announcement, the vertices do not have the knowledge of $n$, and we consider an alternative measure: the average, over the nodes, of the number of rounds before they output. We prove that the complexity of a problem can be exponentially smaller with the new measure, but that Linial's lower bound for colouring still holds.