


Dans ce chapitre, nous présentons quelques utilisations que nous avons
pu faire des modèles et opérations présentés tout au long de ce
mémoire. Cela nous permet d’illustrer une nouvelle fois l’intérêt de
la généricité de nos travaux qui peuvent s’appliquer à différentes
dimensions et dans différents domaines, bien que principalement en
modélisation géométrique et traitement d’images 2D et 3D. Nous
présentons également la façon dont nous avons utilisé la méthode
de mise à jour locale des nombres de Betti afin de guider un
algorithme de segmentation d’images 3D en intégrant un critère
topologique. Ce travail est un premier résultat démontrant un apport
important de l’utilisation de modèles combinatoires de haut niveau.
Nous verrons que cela ouvre de nombreuses perspectives prometteuses
sur la poursuite de ces travaux.
Le plan de ce chapitre est le suivant. Nous commençons
Section 7.1 par présenter le modeleur géométrique à base
topologique Moka qui est défini à partir d’un noyau de cartes
généralisées 3D. Ce modeleur est à la base de nombreux travaux, dont
un modeleur de bâtiments. Il est également l’outil d’expérimentation
avec lequel il est facile de tester de nouvelles méthodes. Nous avons
par exemple implanté dans Moka certaines méthodes de calcul
d’invariants topologiques présentés au chapitre 6.
Nous présentons ensuite Section 7.2 l’utilisation des
cartes topologiques 2D et 3D (qui sont définies à partir de noyaux de
cartes combinatoires pour des raisons d’espace mémoire) pour la mise
en œuvre d’algorithmes de segmentation d’images. La
Section 7.3 propose l’extension de ces
méthodes pour la segmentation multi-échelle en utilisant les pyramides
de cartes. Enfin, nous concluons et donnons des perspectives de ce
chapitre à la Section 7.4.
7.1 Modeleur Géométrique
Moka1 est un modeleur géométrique 3D à base
topologique, disponible en téléchargement libre sur
http://moka-modeller.sourceforge.net/. Ce projet a débuté en
1999 durant un stage de Master que j’ai encadré, puis a été poursuivi
dans le cadre du projet RNTL Nogemo de Septembre 2001 à Août 2004. Le
principal développeur a été Frédéric Vidil, ingénieur embauché dans le
cadre de ce projet, et j’ai été le second développeur principal en
collaboration avec Frédéric. Depuis la fin du projet Nogemo, je suis
le chef de projet et le principal développeur de Moka.
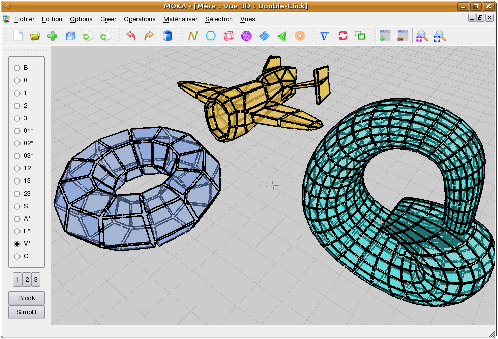
| Figure 7.1: Capture d’écran de Moka avec une scène comportant
différents objets : un tore obtenu par création d’objet de base,
une bouteille de Klein obtenue par extrusion, couture puis
lissage, et un avion obtenu par importation d’un fichier au
format off. |
Ce modeleur se base sur un noyau de 3G-cartes qui fournit les
opérations de manipulations de base des objets 3D. Plusieurs
surcouches ont été développées afin d’enrichir ce noyau de nombreuses
fonctionnalités. Moka contient actuellement plus de 20 types
d’opérations différentes, qui se déclinent pour la plupart en
plusieurs variantes selon la dimension ou selon plusieurs options
(cf. Figs. 7.2 et 7.3 pour quelques exemples
d’opérations). Ces opérations principales peuvent être regroupées en
grandes catégories :
-
les opérations de création d’objets : courbes polygonales,
polygones, cubes, sphères, cylindres, pyramides, tores, avec à
chaque fois la possibilité de fixer le nombre de subdivisions des
objets ainsi que leurs paramètres géométriques ;
- les coutures (mise en relation d’objets par identification de
cellules), décousures (les opérations inverses) ;
- les modifications géométriques : translations, rotations,
homothéties, et plaquages d’un objet le long d’un autre ;
- les opérations de base présentées au
chapitre 3 : suppressions, contractions et
insertions de cellules ;
- les opérations de modifications : triangulations,
quadrangulations, fermetures (la i-fermeture est une opération
rendant une G-carte i-fermée en ajoutant des i-cellules et les
cousants aux i-bords) ;
- le calcul de G-carte duale, en 2D et 3D ;
- les extrusions qui peuvent être simples, le long d’un chemin ou
par révolution ;
- le chanfreinage (ou arrondi) de sommets ou d’arêtes ;
- les maillages ou lissages qui permettent de raffiner une
subdivision, avec dans le cas des lissages une modification de la
géométrie pour obtenir des formes plus arrondies ;
- les opérations booléennes qui sont primordiales dans un
modeleur, et qui permettent l’union, l’intersection et la différence
d’objets.
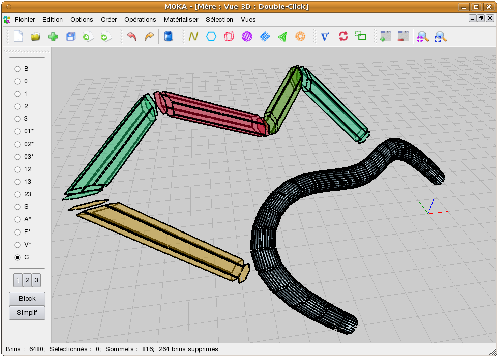
| Figure 7.2: Exemple d’extrusion le long d’un chemin. Le résultat
obtenu est ensuite lissé. |
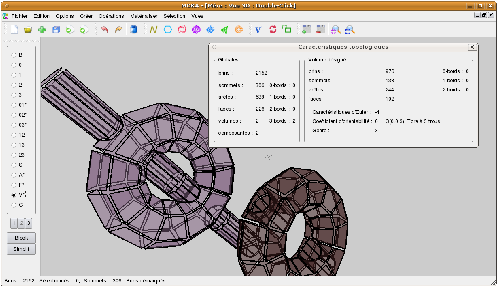
| Figure 7.3: Exemple d’opération booléenne entre un tore et un
cylindre. Nous avons ici conservé l’union des deux objets, et
le résultat du tore moins le cylindre. La boîte de dialogue
montre le calcul du nombre de cellules et de la caractéristique
d’Euler-Poincaré de ce résultat qui est un tore à trois trous. |
De par sa richesse en fonctionnalités et sa stabilité, Moka est un
outil d’expérimentation très riche dans lequel il est facile
d’intégrer et tester de nouvelles méthodes issues de
problématiques de recherche. Nous avons par exemple intégré dans
Moka la plupart des méthodes de calcul d’invariants topologiques
présentées au chapitre 6. Nous avons pu ainsi tester
nos algorithmes de simplification en forme minimale, en utilisant les
invariants topologiques pour vérifier que la topologie des objets est
préservée durant les simplifications.
Enfin, de par sa généricité et son nombre important de
fonctionnalités, Moka a servi de base de développement à plusieurs
projets de modélisation géométrique. La plupart du temps, ces projets
ont des contraintes spécifiques, qu’il suffit de rajouter dans une
surcouche spécifique, mais les opérations de base restent valides et
utilisables. Les principaux projets ayant utilisé Moka sont VORTISS,
un projet labélisé à l’ANR MDCA, dont l’objectif est la reconstruction
d’organes pour l’interaction temps réel en simulation chirurgicale ;
un projet de générateur d’évolutions géologiques par animation basée
sur la topologie [LSM08, LSM09] ; un projet de nomination
persistante afin de faire du suivi d’objets et de la réévaluation de
modèles [BMSB07] ; un projet de modélisation géométrique du
sous-sol [BSP+04] ; un modeleur hiérarchique de complexes
architecturaux [Fra04, FML06].
Parmi ces projets, j’ai participé à l’encadrement de la thèse de
Sébastien Horna [Hor08] dont l’objectif était de proposer une
méthode de reconstruction topologique de complexes architecturaux 3D à
partir de plans numériques 2D [HDMB07, HMDB09]. Nous avons
pour cela mis en œuvre un outil de reconstruction de
bâtiments 3D en utilisant les informations contenues dans les plans
d’architecte, et en contrôlant la validité du résultat obtenu grâce à
des contraintes métier. Nous avons proposé des opérations
automatiques, mais aussi certaines opérations semi-automatiques
permettant d’aider et de guider la reconstruction d’un bâtiment
complet en un nombre réduit d’interactions.
La reconstruction est réalisée en plusieurs étapes, chacune utilisant
des opérations de base de Moka et des propriétés des G-cartes afin de
contrôler la validité de la subdivision obtenue. Durant ce processus,
les opérations géométriques sont toutes réalisées en Epsilon
geometry [SSG89] (test d’intersection, de colinéarité,
trouver les mêmes sommets…). Avant de débuter le processus de
reconstruction, les plans d’origine doivent tout d’abord être importés
dans Moka. Ces plans sont au format DXF (Drawing eXchange
Format) qui est un format très répandu en CAO (cf. Fig. 7.4
pour quelques exemples). Les données récupérées sont un ensemble de
segments qui représentent les plans, et nous construisons alors une
G-carte dans Moka qui contient une arête pour chaque segment.
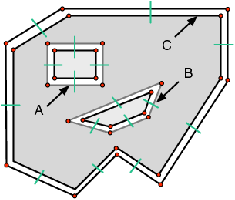
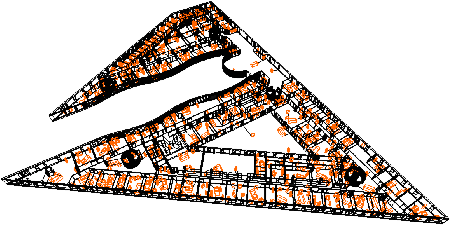
| Figure 7.4: Exemple de plans 2D traités :
(a) Étage 3 Sp2mi, 8120 brins ;
(b) LEA, 17168 brins ;
(c) LR, 25976 brins ;
(d) Étage 0 Sp2mi, 33508 brins. |
Nous avons à ce stade un ensemble une G-carte composée d’arêtes
déconnectées. Le processus de reconstruction d’un modèle valide 2D est
découpé en 5 étapes :
-
traitement des superpositions et intersections d’arêtes ;
- 1-couture des arêtes pour reconstruire les faces ;
- liaison des composantes connexes par des arêtes fictives ;
- détection et correction des arêtes pendantes ;
- affectation de la sémantique des faces.
La première étape consiste à corriger les problèmes
géométriques de l’ensemble des segments. En effet, l’objectif initial
des architectes lors de la création des plans est d’avoir un résultat
visuel satisfaisant. Peu importe alors que deux arêtes soient
superposées, ou que deux arêtes se croisent en dehors de leurs
extrémités. Mais ces cas posent problème dans notre approche car ils
empèchent de garantir que nous reconstruisons bien une partition de
l’espace. Afin de résoudre ces problèmes, chaque couple d’arêtes
supperposées est traité et corrigé de la manière détaillée
Fig. 7.5. Comme la complexité de ce processus est
quadratique en le nombre total d’arêtes, nous avons utilisé une grille
régulière afin d’accélérer les temps de calcul en limitant la
recherche à un petit nombre d’arêtes.
[a]

[b]

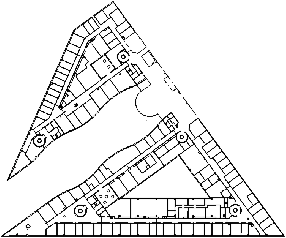
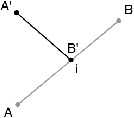
| Figure 7.5: Résolution des problèmes d’arêtes supperposées.
(a) Lorsqu’une arête est incluse dans une autre, elle est
supprimée. (b) Lorsqu’une arête a une partie en commun avec une
autre, elle est réduite afin de supprimer cette partie. Le choix
de l’arête à réduire n’importe pas dans le résultat final. En
effet, le sommet de l’arête qui a été déplacé (A′ sur cet exemple)
sera inséré à nouveau, lorsque c’est nécessaire, par la phase
traitant les problèmes d’intersection d’arêtes. |
Le traitement des problèmes d’intersection d’arêtes est réalisé en
testant si l’intersection entre chaque couple d’arêtes est vide ou est
une extrémité des deux arêtes. Lorsque ce n’est pas le cas, les deux
arêtes s’intersectent en dehors de leurs extrémités. Le problème est
alors résolu en insérant un sommet sur l’une ou sur les deux arêtes
selon les configurations qui sont détaillées
Fig. 7.6. Comme pour le traitement des arêtes
confondues, nous utilisons également une grille régulière afin
d’accélérer la recherche sur les couples d’arêtes ayant une
intersection non vide.
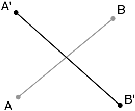
| Figure 7.6: Résolution des problèmes d’intersection
d’arêtes. (a) Lorsque deux arêtes s’intersectent en leurs milieux,
(b) il faut insérer un sommet au point d’intersection sur les deux
arêtes. (c) Lorsque deux arêtes s’intersectent en l’extrémité de
l’une mais pas de l’autre, (d) il faut insérer un sommet seulement
sur une arête. |
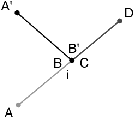
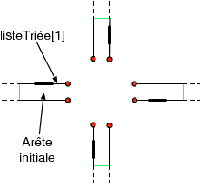
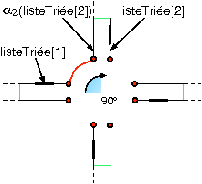
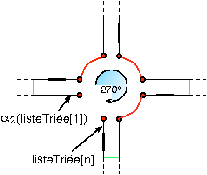
Nous avons maintenant un ensemble d’arêtes disjointes sans problème
géométrique. Nous passons alors à la seconde phase qui consiste à
relier ces arêtes entres elles afin de former des faces. Nous
utilisons pour cela un algorithme d’interclassement qui consiste à
trier angulairement les arêtes incidentes à un même sommet, puis à les
relier deux à deux par α1 en cousant à chaque étape l’arête
courante avec la prochaine arête dans l’ordre angulaire. Après avoir
traité toutes les arêtes du sommet, il reste à fermer la boucle en
cousant la dernière arête avec la première. Ce processus est illustré
Fig. 7.7. Après avoir traité toutes les arêtes de
la G-carte, nous avons défini les liaisons α1 de chaque brin, ce
qui fait que la G-carte est désormais 1-fermée. Comme elle était 0- et
2-fermée par construction (chaque arête est créée avec quatre brins et
ses liaisons α0 et α2), la 2G-carte est donc fermée.
Durant ce processus, nous devons trouver toutes les arêtes qui
partagent une même extrémité, et à nouveau l’utilisation d’une grille
régulière permet d’accélérer cette recherche en la limitant aux brins
appartenant à la même cellule de la grille. Il faut noter que ce
travail pourrait sans doute être amélioré en utilisant un algorithme
de calcul d’arrangements de segments [EGS90], ainsi
qu’en utilisant des calculs géométriques exacts [Yap04].
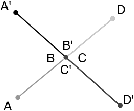
| Figure 7.7: Illustration du processus d’interclassement.
(a) Configuration initiale dans laquelle nous avons un ensemble
d’arêtes partageant une même extrémité. (b) Première liaison par
α1. (c) Résultat après avoir traité toutes les
arêtes. (d) Résultat final après avoir fermé la boucle en cousant
la dernière arête avec la première. |
L’étape suivante consiste à corriger le problème survenant lorsque la
G-carte est composée de plusieurs composantes connexes. En effet,
comme expliqué au chapitre 4 dans le cadre des cartes
topologiques, ces différentes composantes sont déconnectées et sans
lien entre elles. De ce fait, les faces de la subdvision ne sont pas
correctement représentées dans la carte. La solution utilisée ici est
à nouveau l’ajout d’arêtes fictives rendant la carte connexe, et liant
entre elles les différentes composantes connexes
(cf. Fig. 7.8). Pour chaque composante connexe
C, une recherche est effectuée afin de trouver la face contenant
géométriquement C. Une arête fictive est alors insérée entre la face
externe de la composante connexe et sa face englobante. Les sommets
support de cette arête sont choisi de telle manière d’éviter que
l’arête insérée intersecte une autre arête (cf. [Hor08] pour
plus de détails).
[a]
[b]
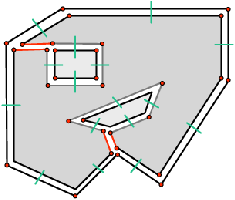
| Figure 7.8: Ajout d’arêtes fictives pour rendre la carte connexe.
(a) Configuration initiale composée de trois composantes
connexes. (b) Carte finale après avoir inséré deux arêtes
fictives. |
Le dernier problème pouvant se poser est la présence d’arêtes
pendantes. Ce problème est lié à l’application car ce type d’arête
correspond ici à une incohérence qui est due à une imprécision
numérique ou à l’omission d’un objet par l’architecte (cf. quelques
exemples Fig. 7.9).
[a]
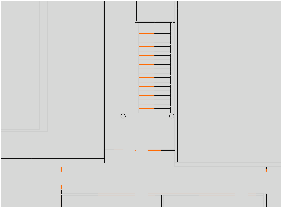
[b]
| Figure 7.9: Exemple d’arêtes pendantes (en rouge) détectées dans un
plan 2D. (a) Des erreurs numériques font que les arêtes associées
aux marches de l’escalier ne touchent pas le rectangle englobant.
(b) Un exemple d’objet manquant, ici probablement une porte. |
La correction de ce problème dépend du contexte de l’arête pendante et
ne peut pas être réalisée de manière totalement automatique. En effet,
selon les cas, cette correction va consister à :
-
prolonger l’arête pendante jusqu’au segment le plus proche, en
ajoutant un sommet au niveau de l’intersection si nécessaire, et
cousant correctement cette arête au niveau de l’intersection ;
- prolonger un ensemble d’arêtes pendantes afin qu’elles
s’intersectent sur un même sommet, en cousant ces arêtes entre elles
au niveau de l’intersection ;
- supprimer l’arête pendante ;
- insérer une porte ou une fenêtre incidente à l’arête pendante ;
- épaissir l’arête pendante pour construire un mur.
Ces quatre opérations sont proposées à l’utilisateur, avec des
variantes permettant par exemple d’appliquer simultanément un ensemble
d’opérations, ou d’essayer automatiquement de prolonger chaque arête
pendante en dessous d’un seuil donné afin de corriger automatiquement
les arêtes très proches qui sont souvent issues d’erreurs de précision
numérique.
Nous avons désormais une partition 2D valide. La dernière étape
consiste à associer une sémantique à chaque face qui sera utilisée
ensuite lors de l’extrusion du plan afin de construire le modèle 3D.
Nous avons défini des étiquettes sémantiques (mur, façade, sol,
plafond, porte, fenêtre, escalier, pièce), chaque face de la carte
étant associée avec exactement une étiquette. Nous avons ensuite
défini des contraintes de voisinage (par exemple une porte doit être
adjacente à deux murs et deux pièces) et nous utilisons ces
contraintes afin de déterminer automatiquement le plus d’étiquettes
sémantiques possible. Nous commençons par affecter la façade car nous
savons que c’est la face externe de la 2G-carte, qui se retrouve
simplement en utilisant les coordonnées des sommets.
Ensuite, nous avons défini un algorithme de propagation des
sémantiques qui utilise les contraintes de voisinages pour propager
les valeurs sémantiques de proche en proche. Enfin, nous avons proposé
des heuristiques permettant de déterminer automatiquement les
étiquettes sémantiques non affectées en utilisant des caractéristiques
géométriques des faces (par exemple des coefficients d’élongation, le
co-degré des faces…). Nous avons offert la possibilité à
l’utilisateur de vérifier et corriger la sémantique associée à chaque
élément du modèle, tout en contrôlant à chaque fois que les
contraintes de voisinages soient respectées.
[a]
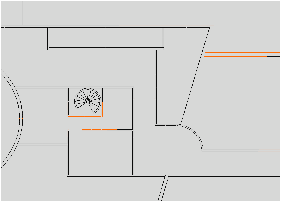
[b]
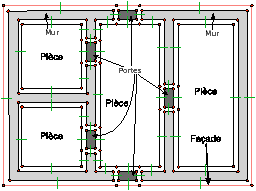
| Figure 7.10: Résultat obtenu à la fin des 5 étapes de reconstruction du
modèle 2D. (a) Le plan initial. (b) La 2G-carte reconstruite avec
sa sémantique associée. |
À la fin des cinq étapes de reconstruction 2D, nous obtenons une
2G-carte valide correspondant au plan initial, avec une sémantique
associée à chacune de ses faces (cf. Fig. 7.10). Nous avons
désormais toutes les informations nécessaires afin de transformer ce
modèle en bâtiment 3D. Cette reconstruction 3D se décompose à son
tour en trois étapes :
-
extrusion du modèle 2D en tenant compte de la sémantique ;
- création d’un volume sol et d’un volume plafond ;
- superposition de plusieurs étages ;
- ajout des escaliers entre les étages.
La première étape est l’extrusion du modèle 2D qui permet de
le convertir en modèle 3D. Comme nous pouvons voir
Fig. 7.11, il existe trois types d’extrusion selon la
sémantique de la face. L’opération d’extrusion existe déjà dans Moka,
la seule difficulté est ici de l’appeler avec les bons paramètres,
puis ensuite de relier les différents volumes issus des trois types
d’extrusion. Après cette étape, nous obtenons un modèle 3D où chaque
face du plan 2D est devenue un volume 3D. Durant cette étape
d’extrusion, nous propageons correctement la sémantique des faces aux
volumes créés.
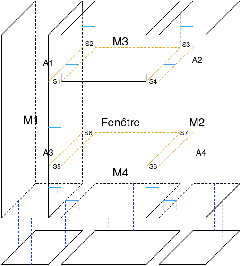
| Figure 7.11: Les trois types d’extrusion possibles en fonction de la
sémantique des faces. (a) Cas général (pièce, mur, façade) :
extrusion le long d’un chemin composé d’une seule arête. (b) Cas
d’une porte : extrusion le long d’un chemin composé de deux
arêtes. La première arête pour la porte elle-même, la seconde pour
le pan de mur au dessus de la porte. (c) Cas d’une fenêtre :
extrusion le long d’un chemin composé de trois arêtes. La première
arête pour le mur en dessous de la fenêtre, la seconde pour la
fenêtre elle-même, et la troisième pour le mur au dessus de la
fenêtre. |
La seconde étape consiste à créer un volume sol et un volume plafond
en dessous (resp. en dessus) du résultat de l’extrusion. Ces volumes
sont construits à partir d’une copie des faces inférieures
(resp. supérieures) de l’étage, comme illustré
Fig. 7.1. Ces volumes ont deux raisons d’être : la
première raison est physique, car ils correspondent à la réalité d’un
bâtiment et peuvent avoir un impact, par exemple sur des simulations
de propagation d’ondes. La seconde raison est qu’ils servent lors de
la superposition de plusieurs étages. En effet, comme illustré
Fig. 7.12, lorsque les deux étages ont la même
géométrie, cette superposition revient à supprimer la face supérieure
du plafond du premier étage, et la face inférieure du sol de l’étage à
superposer, puis à relier entre elles les faces qui étaient incidentes
à ces faces supprimées.
| Figure 7.12: Sol, plafond et superposition d’étages. (a) Illustration
des volumes sol et plafond. (b) Configuration initiale avant la
superposition. (b) La face supérieure du plafond et la face
inférieure du sol sont supprimées. (c) Les faces adjacentes sont
reliées entre elles. |
Lorsque les étages ont des géométries différentes, une étape
supplémentaire est nécessaire afin de découper la géométrie de la face
entre les deux étages, de manière à créer une sous-partie
identique. Cette découpe s’effectue au moyen des opérations
d’insertion de sommet et d’arête. C’est ensuite le long de cette
partie commune que les étages sont superposés en se ramenant au cas
précédent où les deux étages avaient la même géométrie
(cf. Fig. 7.13 pour deux exemples d’étages
superposés).
[a]
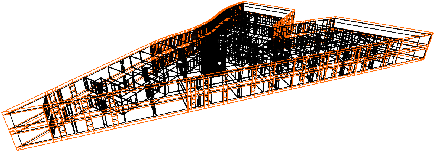
[b]
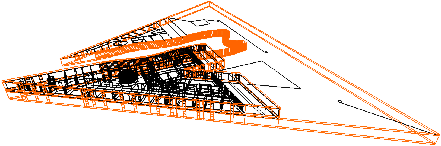
| Figure 7.13: Deux exemples de résultats obtenus après extrusion et
superposition de deux étages. (a) Cas de deux étages ayant la même
géométrie. (b) Cas de deux étages ayant des géométries
différentes. |
La dernière étape du processus de reconstruction 3D consiste à relier
les étages entre eux en insérant des escaliers. Ces escaliers sont
présents dans les plans 2D, et détectés automatiquement durant la phase
d’assignation de sémantique par la présence de nombreuses petites
faces similaires, en tenant compte des différents types d’escaliers
possibles (droits, colimaçons…). Les faces étiquetées escalier ne
sont pas extrudées durant l’étape précédente, et les escaliers sont
construits par un algorithme spécifique. Afin de relier les étages entre
eux, l’étage supérieur est découpé par un volume obtenu par extrusion
de la forme de l’escalier dans le plan 2D, en utilisant les opérations
booléennes de Moka (et plus précisément la soustraction,
cf. Fig. 7.14 pour deux illustrations).
[a]
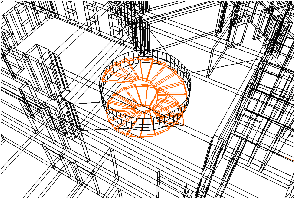
[b]

| Figure 7.14: Visualisation du résultat d’insertion d’un escalier en
colimaçon entre deux étages. |
Nous avons également proposé d’autres opérations (non détaillées ici)
permettant de finaliser le modèle 3D, comme la construction de toit
qui est basée sur l’opération de chanfreinage, ou d’autres opérations
de modification permettant à l’utilisateur de modifier soit le plan 2D
reconstruit, soit directement le modèle 3D à la fin de l’ensemble de
la reconstruction. Nous pouvons par exemple citer les fusions et
découpes de pièces qui s’appuient sur les opérations de suppression et
d’insertion, les translations de murs avec contraintes, la
simplification et à l’inverse la triangulation des scènes, ou encore
l’ameublement automatique (cf. Fig. 7.15), ou une
visualisation interactive. Pour toutes ces opérations, nous utilisons
à chaque fois différentes cellules de la subdivision, ainsi que les
relations d’adjacence et d’incidence entre ces cellules, ce qui montre
l’intérêt d’utiliser un modèle combinatoire décrivant toutes ces
informations.
| Figure 7.15: Exemple de résultat obtenu après l’opération d’ameublement
automatique. (a) Pour le bâtiment LEA. (b) Pour le bâtiment
Étage 0 Sp2mi. |
Grâce à toutes ces opérations, nous disposons d’une chaîne complète de
traitement partant de la reconstruction de bâtiments à partir de
données numériques 2D jusqu’à la visualisation de ces environnements
en utilisant une méthode de lancer de rayons interactive. Le point fort
de notre approche est que chaque étape composant la chaîne de
reconstruction utilise des contraintes géométriques, topologiques et
sémantiques de notre modèle, ce qui garantit l’obtention d’un modèle
valide. Nous pouvons voir Fig. 7.16 quelques résultats de
reconstruction obtenus.
| Figure 7.16: Bâtiments 3D reconstruits à partir de plans numériques, et
visualisés avec le logiciel Pov-ray. |
7.2 Segmentation d’Images
Notre deuxième champ d’expérimentation privilégié est le traitement
d’images, en suivant et étendant l’idée initiale qui était d’utiliser
un graphe d’adjacence de régions pour la résolution de problématiques
de traitement d’images. Nous avons utilisé le modèle des cartes
topologiques et les opérations proposées au chapitre 4
afin de mettre en œuvre des algorithmes de segmentation
d’images. Nous avons tout d’abord adapté l’algorithme proposé dans
[FH98, FH04], qui est basé sur une segmentation par
croissance de régions en utilisant un critère basé sur la notion de
contraste d’une région définie sur un graphe.
De manière simplifiée, la méthode originale consiste à associer un
sommet du graphe à chaque pixel de l’image, à mettre une arête entre
chaque couple de pixels 4-voisins (la méthode initiale était proposée
en 2D), et à associer un poids à chaque arête, qui est une mesure non
négative de dissimilarité entre les éléments associés aux deux sommets
extrémités de l’arête. Avec ce formalisme, une segmentation de
l’image est induite par un sous-ensemble d’arêtes : chaque composante
connexe dans le sous-graphe induit par cet ensemble d’arêtes correspond
à une région de la segmentation. Dans la méthode originale, les
auteurs utilisent deux prédicats pour mesurer la dissimilarité des
régions : le contraste interne à une région Int(R) qui est le poids
de l’arête de coût maximum dans l’arbre couvrant de poids minimum des
arêtes de cette région ; et le contraste externe entre deux régions
Ext(R1,R2) qui est le poids de l’arête de coût minimum entre R1
et R2.
Deux régions R1 et R2 sont considérées comme similaires si
Ext(R1,R2)>MInt(R1,R2), avec
MInt(R1,R2)=min(Int(R1)+τ(R1), Int(R2)+τ(R2)) qui est le
plus petit contraste interne des régions R1 et R2 pondéré par
une fonction τ qui permet de paramétrer l’algorithme.
Le rôle de τ est de mitiger l’estimation du contraste interne
lorsque celui-ci n’est pas représentatif comme par exemple pour les
petites régions. Les auteurs suggèrent d’utiliser une fonction
τ(R) = k / |R| avec |R| le nombre de pixels de R, et k une
constante qui définit l’échelle de segmentation : en augmentant k,
le nombre de régions fusionnées va augmenter. N’importe quelle
fonction à valeurs positives peut être utilisée pour τ.
Dans leur article, les auteurs établissent une notion de segmentation
optimale (pour le critère donné) qui est une segmentation n’ayant pas
deux régions voisines pouvant fusionner (segmentation appelée
sur-segmentation), ni une région pour laquelle il existe un
raffinement qui n’est pas une sur-segmentation (segmentation appelée
sous-segmentation) et montrent que leur algorithme produit une
segmentation optimale.
Nous avons adapté cet algorithme aux cartes topologiques 2D et 3D, en
modifiant les critères de contraste pour les rendre plus facilement
calculables [DD08b]. Pour cela, nous avons transformé le
contraste externe Ext(R1,R2) en un contraste associé à chaque face
de la carte Ext(f). Nous avons prouvé que le contraste externe entre
R1 et R2 est égal au plus petit des contrastes de toutes les
faces entre ces deux régions. Avec cette modification, nous pouvons
associer chaque contraste externe aux faces de la carte topologique,
et chaque contraste interne aux régions. De ce fait, étant donné un
brin, nous retrouvons en O(1) ces deux valeurs.
L’Algorithme 7.2 présente la segmentation d’une
image par critère de contraste à l’aide d’une carte topologique. Il
prend en paramètre une carte topologique M représentant une
sur-segmentation d’une image et modifie la carte afin que la partition
représentée soit optimale. Cet algorithme est donné ici en 3D mais est
directement modifiable en dimension n, en remplaçant β3(b) par
βn(b), et en associant le contraste externe aux
(n−1)-cellules. Nous avons également prouvé dans [DD08b] que
cet algorithme est équivalent à l’algorithme original.
| Figure 7.17: Algorithme : Segmentation par critère de contraste |
-
Entrées : Une carte topologique 3D M.
- Résultat : M représente la segmentation optimale de l’image.
L ← liste triée des faces;
Tant que L n’est pas vide faire
b ← défiler L;
f ← face(b);
R1 ← region(b); R2 ← region(β3(b));
Si R1 ≠ R2 alors
Si Ext(f) ≤ MInt(R1,R2) alors
R ← fusionner symboliquement R1 et R2;
Int(R) ← Ext(f);
fusion effective des régions dans la carte topologique;
Cet algorithme utilise l’opération de fusion globale évoquée
Section 4.5.2, la seule différence porte sur
l’initialisation des arbres union-find qui est réalisée au moyen des
critères de contraste. Cet algorithme montre à nouveau l’intérêt des
cartes topologiques qui autorisent la manipulation de différentes
cellules (ici les régions et les faces entre les régions) en décrivant
les relations d’adjacence et d’incidence entre ces cellules. Nous
avons intégré cette méthode à nos deux logiciels permettant de
calculer les cartes topologiques 2D et 3D à partir d’images
(cf. Fig. 7.18 pour une capture d’écran du logiciel 3D)
et effectué plusieurs expérimentations afin d’étudier l’efficacité de
notre approche. Ces résultats montrent en moyenne que la segmentation
d’une image 3D de taille 256×256×93 est réalisée en 13
secondes ce qui est tout à fait raisonnable sachant que le logiciel
développé est pour le moment un prototype et pourrait bénéficier de
nombreuses optimisations.
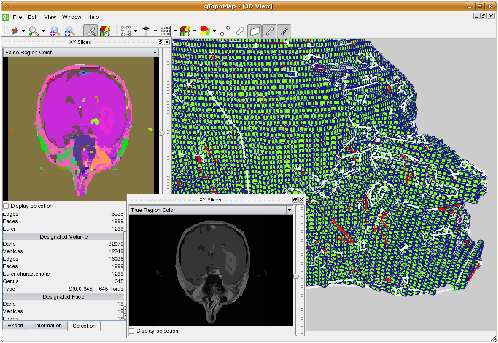
| Figure 7.18: Capture d’écran du logiciel de segmentation d’images 3D
basé sur les cartes topologiques. La région sélectionnée et
affichée en 3D est un tore à 645 tunnels. Nous voyons également
deux plans de coupe XY de l’image segmentée, dont un en fausses
couleurs. |
De plus, nous avons proposé des variantes de cet algorithme, en
modifiant simplement le critère utilisé pour autoriser la fusion, afin
par exemple de proposer un algorithme fusionnant chaque région de
taille inférieure à un seuil donné avec la région la plus proche dans
son voisinage. Cette opération permet de supprimer rapidement toutes
les petites régions obtenues après une passe de segmentation, qui sont
souvent issues de bruit.
Nous avons proposé dans [DD09] une variante particulièrement
intéressante, et justifiant l’intérêt d’un modèle topologique, qui
consiste à intégrer un critère topologique à l’algorithme de
segmentation. Nous avons pour cela utilisé la méthode de calcul
des nombres de Betti des régions de la carte topologique
présenté Section 6.3, et avons montré comment utiliser
ces nombres de Betti au sein du critère de segmentation. Notre idée
est de contrôler l’évolution des nombres de Betti durant la
segmentation afin de guider le résultat en fonction de connaissance
a-priori. Un exemple d’utilisation pourrait être la segmentation du
cortex cérébral sur les images IRM, où un résultat connu en médecine
dit que chaque hémisphère du cortex est homéomorphe à une sphère sans
cavité. En intégrant un critère topologique basé sur les nombres de
Betti, nous pouvons garantir que le résultat produit par la
segmentation vérifie cette propriété.
Pour mettre en place ce contrôle, nous conservons le même algorithme
de segmentation que nous venons de présenter, en modifiant simplement
le critère utilisé lors de la fusion symbolique. Durant l’exécution
de cet algorithme, pour chaque face courante incidente à R1 et R2,
nous effectuons les quatre étapes suivantes :
-
évaluation d’un critère valeur (par exemple le critère de
contraste) sur R1 ∪ R2 ;
- si le critère valeur est vrai, mise à jour locale des nombres de
Bettu pour calculer b1(R1 ∪ R2) et b2(R1
∪ R2) ;
- évaluation d’un critère dit topologique utilisant les valeurs de
b1 et de b2 calculées ;
- si le critère topologique est vrai, fusion symbolique de R1
avec R2 et propagation des valeurs nécessaires à l’algorithme de
calcul des nombres de Betti.
Le premier test utilise un critère valeur classique, par
exemple celui à base des contrastes, afin de fusionner des zones
homogènes de l’image. Lorsque ce critère est satisfait, nous calculons
les nombres de Betti de la région que nous obtiendrions comme résultat
de la fusion en utilisant la méthode de mise à jour locale, et
vérifions si le critère topologique sur cette éventuelle future région
est satisfait. Lorsque c’est le cas, la fusion symbolique est
réalisée.
Nous avons proposé différents types de critères topologiques, qui
peuvent contrôler l’évolution des tunnels avec b1 et/ou des
cavités avec b2. Ces critères peuvent être :
-
non évolution : bi(R1 ∪
R2)=bi(R1)+bi(R2) ; pour ne pas autoriser la
modification du nombre de tunnels ou de cavités ;
- non croissance :bi(R1 ∪
R2)≤bi(R1)+bi(R2) ; pour ne pas créer de
nouveau tunnel ou cavité (de manière similaire nous pouvons définir
la non décroissance) ;
- convergence vers ki donné par l’utilisateur : |bi(R1
∪ R2)−ki|≤ |bi(R1)+ bi(R2)−ki| ; pour que la
fusion fasse converger le nombre de tunnels ou de cavités vers un
seuil.
Il est simple de définir d’autres critères, voire de combiner les deux
nombres de Betti afin par exemple d’autoriser les objets pour lesquels
la somme des nombres de tunnels et de cavités est inférieure à un
seuil donné.
Afin de réaliser ce critère topologique, nous calculons les nombres de
Betti de R1 ∪ R2 au cours de l’étape de la fusion symbolique,
sans réaliser effectivement cette fusion, ce qui est beaucoup plus
efficace. Par contre, cela demande à modifier le parcours de surface
utilisé lors de la mise à jour locale des nombres de Betti afin de
parcourir les régions résultantes de la fusion symbolique. Il suffit
pour cela de traverser également les brins des faces internes des
régions, c’est-à-dire les faces incidentes à un brin b tel que
find(region(b))=find(region(β3(b))). Traverser ces faces revient
à parcourir le chemin de connexion entre les brins situés autour de
celles-ci, ce qui nous ramène bien au parcours des brins de la surface
obtenue après la suppression des faces internes.
Nous avons effectué plusieurs tests afin d’étudier l’impact du critère
topologique sur le résultat de segmentation. Nous pouvons voir
Fig. 7.19 un exemple obtenu avec une image
artificielle en utilisant un critère topologique interdisant à
b1 de dépasser un certain seuil. Nous voyons sur cet exemple
l’impact du critère topologique qui entraîne différents
résultats. Comme ici le critère utilisé interdit strictement à
b1 de dépasser le seuil, nous garantissons que chaque région
du résultat a bien un b1 inférieur ou égal au seuil. Ce
résultat dépend toutefois de la partition initiale. En effet, il est
garanti uniquement si chaque région de la carte initiale est
homéomorphe à une boule sans cavité. Si ce n’est pas le cas, nous ne
pourrons pas, avec cette méthode, garantir de propriétés sur chaque
région.
[a
]

[b
]

[c
]

[d
]

| Figure 7.19: Expériences avec une image 3D artificielle, en utilisant un
critère topologique interdisant à b1 de dépasser un
certain seuil k (la région de fond n’est pas représentée afin
d’observer ce qui se passe sur la région claire).
Figure 7.2 Image originale. Chaque
voxel de l’image appartient à une région différente.
Figure 7.2 Résultat avec k=0. L’objet
est représenté par trois régions, chacune n’ayant pas de tunnel.
Figure 7.2 Résultat avec k=1.
L’objet est représenté par deux régions, une ayant un tunnel,
l’autre non. Selon l’ordre des fusions (qui dépend de la couleur
des voxels) nous aurions pu obtenir deux régions sans tunnel, ou
deux régions à un tunnel.
Figure 7.2 2-tore obtenu lorsque nous
n’utilisons pas de contrainte sur les nombres de Betti. |
7.3 Segmentation Multi-échelles
Nous avons utilisé les pyramides généralisées afin de mettre en place
un outil de segmentation multi-échelle d’images 3D [SD06].
La construction d’une telle pyramide se base sur le même principe que
celui utilisé lors de la définition des cartes topologiques 3D pour
simplifier une carte en sa forme minimale, ainsi que sur l’algorithme
de segmentation d’une carte présenté section précédente. L’intérêt de
conserver plusieurs niveaux de segmentation d’une même image est de
pouvoir ensuite travailler en parallèle sur plusieurs niveaux de
segmentation différents, de choisir la segmentation la plus adaptée à
l’opération effectuée, ou d’effectuer un traitement préliminaire sur
une segmentation relativement grossière qui va donc demander moins de
ressources, puis de concentrer les traitements de manière locale sur
une segmentation plus fine.
La pyramide de cartes généralisées utilisée dans le cadre de la
segmentation multi-échelle d’une image 3D représente chaque niveau de
segmentation et permet une navigation entre les niveaux de
segmentation mais aussi entre les cellules les composant. La
construction de cette pyramide est réalisée à partir d’une première
carte qui représente soit chaque voxel de l’image dans sa propre
région, soit qui est une pré-segmentation de l’image initiale en un
grand nombre de régions. Le choix de la méthode initiale dépendra de
la taille des images à traiter et du niveau de bruit.
Ensuite, l’ajout d’un nouveau niveau de segmentation est obtenu en
trois étapes :
-
fusion des régions adjacentes et similaires selon un critère
donné : la fusion est réalisée en supprimant chaque face entre deux
régions à fusionner ;
- simplification des faces : suppression de chaque arête
supprimable qui est de degré deux ou pendante ;
- simplification des arêtes : suppression de chaque sommet
supprimable qui est de degré deux.
En n’effectuant qu’un seul type de suppression à la fois, l’ajout d’un
k-ième niveau de segmentation d’une image est réalisé par l’ajout de
trois nouveaux niveaux dans la pyramide :
-
le premier, noté niveau 3k, représente les régions de la
nouvelle segmentation issues de la fusion des régions du niveau
précédent. Le bord de chaque région de ce niveau est constitué des
faces, arêtes et sommets composant le bord de l’union des régions
fusionnées pour la former ;
- le deuxième, noté niveau 3k+1, représente la nouvelle
segmentation avec cette fois un nombre minimal de faces ;
- le troisième, noté niveau 3k+2, représente la nouvelle
segmentation avec un nombre minimal de faces, d’arêtes et de
sommets.
La pyramide permettant de représenter différents niveaux de
segmentation d’une même image 3D peut être définie formellement de la
manière suivante.
Définition 84 (Pyramide généralisée 3D en segmentation multi-échelle)
Soit k ≥ 1.
La pyramide généralisée représentant les k niveaux de segmentation
d’une image 3D est l’ensemble P = {Ga, Aa}0 ≤ a ≤
3k−1 où :
-
G0 est une 3-G-carte représentant un premier niveau de
segmentation obtenu par fusion des voxels de l’image;
- ∀ a, 0 ≤ a < 3k−1
-
si a = 0 (mod 3 ), Sa = S1a est l’ensemble des arêtes
supprimables et de degré deux ou pendantes ;
- si a = 1 (mod 3 ), Sa = S0a est l’ensemble des
sommets supprimables et de degré deux ;
- si a = 2 (mod 3 ), Sa = S2a est l’ensemble des faces
séparant deux régions similaires selon un critère de
segmentation ;
- ∀ a, 0 ≤ a < 3k−1, Ga+1 est obtenue à partir
de Ga en supprimant les cellules de Sa;
- ∀ a, 0 ≤ a ≤ 3k−1, Aa est l’arbre
d’imbrication des régions de Ga.
Le critère de segmentation utilisé pour construire chaque nouveau
niveau de segmentation peut-être celui présenté à la section
précédente basé sur les contrastes ou un autre, et il peut
éventuellement intégrer un critère de contrôle topologique. En effet,
tout les travaux présentés dans les chapitres précédents (calcul des
cartes topologiques et des invariants topologiques) s’étendent
directement aux pyramides puisque chaque niveau est une carte
généralisée. De plus, ces travaux peuvent souvent être optimisés en
utilisant le modèle hiérarchique afin de propager les calculs et
simplifier les opérations et les parcours. Nos expérimentations de
segmentation hiérarchique 3D se sont pour le moment limitées à des
images artificielles de très faibles tailles, afin de tester et
valider les algorithmes. Ces travaux autour de l’utilisation de ces
pyramides doivent être poursuivis et étendus afin de pouvoir traiter
des images réelles de taille plus importante, et de définir des
méthodes de traitement d’images hiérarchiques.
7.4 Conclusion
Dans ce chapitre, nous avons présenté différentes utilisations des
cartes et des extensions présentées tout au long de ce mémoire. Nos
champs privilégiés d’expérimentation sont la modélisation géométrique
et le traitement d’images. Ces deux thématiques de recherche, a priori
relativement éloignées, se rejoignent dans les besoins de décrire des
objets, les cellules des subdivisions, et les relations d’incidence et
d’adjacence entre les cellules. De plus, les opérations spécifiques
développées dans des applications précises se rejoignent souvent dans
l’utilisation d’opérations de base communes (par exemple les
opérations de suppression), et dans les besoins de contrôler
l’évolution des objets durant ces simplifications. Nous avons par
exemple pu voir que le problème de déconnexion se produisant dans le
cadre de la reconstruction de complexes architecturaux est résolu par
l’adjonction d’arêtes fictives qui est la solution utilisée pour
résoudre le même problème dans les cartes topologiques 3D.
Nous avons également vu dans ce chapitre comment mettre en œuvre
un processus de segmentation d’images à l’aide des cartes
topologiques. Dans un premier temps, nous avons simplement porté un
algorithme existant sur les graphes. Mais nos travaux trouvent leur
pleine justification dans l’utilisation d’un critère topologique au
sein de l’algorithme de segmentation. En effet, mettre en place ce
critère nécessite d’être capable de calculer efficacement, donc
localement, l’évolution des caractéristiques topologiques étudiées, ce
qui est possible ici grâce à l’utilisation d’un modèle à base de carte
décrivant la topologie de la subdivision.
Nous avons également utilisé les cartes combinatoires dans différentes
autres applications. Nous pouvons citer un algorithme de remplissage
de l’intérieur de régions [DA07], une méthode de
reconstruction parallèle de contours discrets multi-régions
[DC08], ou encore des méthodes de segmentation d’images 2D
par approches stochastiques à base de chaînes de Markov
[BAD+02, DAB03]. Dans chacun de ces cas, les cartes
permettent de manipuler la subdivision des objets manipulés, d’associer
des informations aux cellules (comme par exemple des équations de
droites discrètes aux arêtes pour la reconstruction parallèle de
contours discrets), et d’utiliser des critères topologiques (comme par
exemple la profondeur dans l’arbre d’imbrication pour le remplissage de
l’intérieur de régions).
Les poursuites possibles de ces travaux sont nombreuses et les
perspectives très riches. Tout d’abord dans le cadre de la
modélisation, nous souhaitons étudier le lien entre les pyramides de
cartes et les opérations de modélisation, afin de pouvoir, à long
terme, proposer un modeleur géométrique qui devrait être l’équivalent
de Moka, mais totalement hiérarchique. Pour cela, nous devons étudier
chaque opération et définir quel est le résultat à produire dans le
cas hiérarchique. L’intérêt de ce type d’opération réside à nouveau
dans les optimisations possibles en effectuant certains calculs à une
faible résolution puis en propageant ces informations de proche en
proche dans les niveaux de la pyramide.
Ces perspectives sont plus importantes concernant le traitement
d’images. En effet, nous avons pour le moment proposé un premier
critère topologique de contrôle de segmentation, et ce travail doit
être poursuivi et développé afin de montrer pleinement son intérêt
dans des problématiques réelles. Pour cela, nous devons travailler en
collaboration avec des spécialistes de traitement d’images, et nous
atteler à la résolution de problèmes concrets dans lesquels nous
sommes convaincus que l’apport d’information topologique peut aider à
améliorer le résultat obtenu. De plus, nous pouvons également
envisager de proposer de nouvelles opérations utiles dans le cadre du
traitement d’images. Nous souhaitons développer de nouveaux critères
de segmentation, utilisant par exemple des critères géométriques sur
la taille ou la forme des frontières entre les régions, mais aussi des
nouvelles opérations semi-interactives afin de permettre à un expert
de corriger simplement le résultat d’une segmentation qu’il ne
trouverait pas satisfaisant. Ce type d’opération rejoint partiellement
les opérations de modélisation géométrique, tout en rajoutant un
contrôle supplémentaire lié au fait que l’espace sous-jacent est
discret. Nous envisageons par exemple une opération de découpe d’une
région 3D, qui serait guidée par la souris de l’expert mais également
par les données images, par exemple en utilisant une image de
gradient, tout en ajoutant un contrôle topologique. Ces travaux
peuvent être très nombreux et trouver des débouchés importants, mais
nécessitent des collaborations avec des spécialistes afin de répondre
à des problématiques précises.
Une dernière perspective de recherche qui est relativement récente
concerne l’intégration d’un noyau de cartes combinatoires dans la CGAL
(Computational Geometry Algorithms Library, cf.
http://www.cgal.org/), une bibliothèque très importante de
géométrie algorithmique. Cette bibliothèque très riche permet pour le
moment, entre autres, de manipuler des triangulations 2D et 3D, et des
subdivisions cellulaires 2D à l’aide d’une structure de demi-arêtes,
mais il n’existe pas de structure pour les subdivisions cellulaires 3D
ce qui peut s’avérer limitant pour ses utilisateurs. Nous avons donc
commencé à développer un noyau de cartes combinatoires pouvant
s’intégrer dans CGAL, en utilisant l’expérience acquise durant le
développement de Moka et des deux programmes autour des cartes
topologiques 2D et 3D. Notre premier objectif est de proposer assez
rapidement un noyau permettant de manipuler des subdivisions nD à
l’aide de n-cartes, puis par intégrer progressivement des opérations
de manipulation et de calcul d’invariants topologiques.









 [b]
[b]
 [d]
[d]
 [b]
[b]

 [b]
[b]
 [c]
[c]
 [d]
[d]
 [b]
[b]
 [c]
[c]
 [d]
[d]
 [b]
[b]

 [b]
[b]

 [b]
[b]

 [b]
[b]
 [c]
[c]
 [b
[b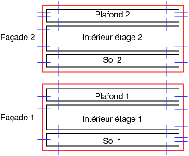 [c
[c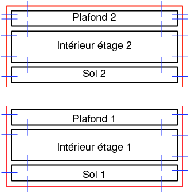 [d
[d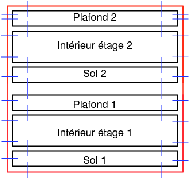
 [b]
[b]

 [b]
[b]






 [b
[b [c
[c [d
[d