


Chapitre 4 Cartes Combinatoires pour Représenter des Images
Dans ce chapitre, nous nous intéressons aux particularités des cartes
combinatoires lorsqu’elles sont utilisées pour représenter des
images. En effet, de par la structure régulière des grilles
considérées, la topologie des partitions représentées possède des
propriétés particulières.
La problématique sous-jacente est la représentation et la manipulation
de régions dans une image étiquetée. En effet, la plupart des
algorithmes de segmentation ont besoin de représenter le résultat de
la segmentation dans une structure de données afin de pouvoir
manipuler les régions obtenues, par exemple pour calculer des
caractéristiques sur ces régions. Ces caractéristiques peuvent être
colorimétriques (par exemple la moyenne des niveaux de gris de la
région), géométriques (par exemple une estimation de la forme de la
région) ou topologiques (par exemple retrouver toutes les régions
adjacentes à une région).
Plusieurs travaux portant sur la définition d’une telle structure
de données ont conclu qu’il était intéressant de représenter les
subdivisions des régions en cellules, et de décrire les relations
d’incidence et d’adjacence entre ces cellules, pour pouvoir ensuite
utiliser ces informations au sein d’algorithmes de traitement
d’images. C’est dans ce cadre que des recherches ont débuté à la fin
des années 1980 sur l’utilisation des cartes combinatoires pour
représenter des images 2D [BG88]. Ces travaux se sont
ensuite développés dans les années 1990 [Fio96, BD99]
notamment durant les trois thèses de Jean-Philippe Domenger
[Dom92], Christophe Fiorio [Fio95] et Luc Brun
[Bru96]. Les cartes combinatoires 2D ont été aussi utilisées
dans des problématiques d’édition d’images
[BG89, GHPVT89, BG91] et de segmentation d’images
[BDB97, BD97, BB98, AFG99, Köt02, BDM03].
Mais il n’existait pas, lorsque j’ai débuté ma thèse, de travaux en
dimension supérieure, et j’ai donc travaillé à la définition d’un
modèle combinatoire de représentation d’une image 3D étiquetée et à
son utilisation au sein d’opérations de traitement d’images. Pour
atteindre cet objectif, j’ai commencé par étudier le problème en 2D
car l’extension des modèles existants était délicate. C’est ce travail
qui m’a amené à la définition des cartes topologiques en 2D et 3D puis
à l’étude d’opérations sur ce modèle.
La principale difficulté, que nous allons retrouver tout au long de ce
chapitre, est la propriété de minimalité des cartes manipulées (en
nombre de cellules). Cette propriété supplémentaire est liée aux
informations sur les régions que nous souhaitons
décrire. Intuitivement, lorsque deux régions sont adjacentes, elles se
touchent par une zone de contact qui doit être représentée par une
seule cellule dans la carte. Cette notion de zone de contact est
formalisée dans ce chapitre par la notion d’arête frontière en 2D et
de face frontière en 3D. Une seconde difficulté concerne les problèmes
de déconnexion susceptibles de se poser durant les
simplifications. Ces problèmes doivent être résolus pour garantir
l’absence de perte d’information durant les simplifications. Ce sont
ces deux problèmes, qui sont d’ailleurs liés, qui rendent difficile la
définition des cartes topologiques et qui étaient bloquants dans
l’extension des modèles existants en 3D. Dans les deux cas,
l’utilisation et le contrôle des opérations de suppression nous à
permis de résoudre les problèmes.
Le plan de ce chapitre est le suivant. Tout d’abord nous commençons
par présenter Section 4.1 les notions préliminaires
liées à la géométrie et topologie discrètes, et nécessaires par la
suite. Puis nous présentons Section 4.2 les modèles
qui existaient avant que nous démarrions nos travaux. Enfin nous
présentons la définition de notre modèle, la carte topologique, tout
d’abord en 2D Section 4.3 puis en 3D
Section 4.4. Nous présentons à la Section 4.5
les opérations d’extraction, de fusion et de découpe définies sur
les cartes topologiques, avant de conclure
Section 4.6 et de donner des perspectives de
recherche à ce chapitre.
4.1 Notions Préliminaires
Nous présentons dans cette section les notions de base utiles dans la
suite de ce chapitre. Un pixel
(resp. voxel) est un point du plan discret
ℤ2 (resp. de l’espace discret ℤ3) avec une valeur qui
peut être une couleur ou un niveau de gris, et une
image de dimension 2 (resp.
dimension 3) est un ensemble fini de
pixels (resp. voxels). Une image
étiquetée est une image dans laquelle chaque
pixel (resp. voxel) est étiqueté. Il n’y a pas de contrainte sur cet
étiquetage, et il est facile d’associer à n’importe quelle image une
image étiquetée simplement en prenant comme étiquette la valeur
associée à chaque pixel (resp. voxel).
La distance l1 entre deux
points p=(p1,…,pn) et q=(q1,…,qn) d’un espace
euclidien est l1(p,q)=∑i=1n|pi−qi|. La distance l∞
est
l∞(p,q)=maxi=1n|pi−qi|.
Deux pixels sont 4-adjacents si la
distance l1 entre les deux pixels égale à un, ils sont
8-adjacents si la distance l∞ est
égale à un. Deux voxels sont 6-adjacents
si la distance l1 entre les deux voxels est égale à un,
26-adjacents si la distance l∞
est égale à un, et 18-adjacents s’ils
sont 26-adjacents et si la distance l1 est inférieure ou égale à
deux. Soit un pixel (resp. voxel) p, son
α-voisinage est l’ensemble des
pixels (resp. voxels) α-adjacents à p. Nous utilisons l’ordre
lexicographique1 pour comparer deux
pixels (resp. voxels).
Un α-chemin de pixels (resp. voxels) est
une suite de pixels (resp. voxels) deux à deux α-adjacents. Une
α-courbe est un α-chemin tel que
chaque pixel (resp. voxel) de la courbe, sauf ses deux extrémités, a
exactement deux points α-adjacents dans la courbe, les deux
extrémités de la courbe ayant exactement un point α-adjacent dans
la courbe. Une α-courbe est fermée
si c’est un α-chemin tel que chaque pixel (resp. voxel) de la
courbe a exactement deux points α-adjacents dans la courbe.
Soit E un ensemble de pixels (resp. voxels). Le
complémentaire de E, noté
E, est l’ensemble des pixels (resp. voxels) de ℤ2
(resp. ℤ3) n’appartenant pas à E. E est un ensemble
α-connexe s’il existe un
α-chemin entre chaque couple de pixels (resp. voxels) ayant
tous ses éléments dans E.
Dans ce travail, nous choisissons de manipuler les ensembles de pixels
4-connexes (resp. voxels 6-connexes). Cela nous amène à la définition
centrale de la notion de région.
Définition 59 (région)
Une région
est un ensemble maximal de pixels
(resp. voxels) 4-connexe (resp. 6-connexe) ayant la même étiquette.
Pour éviter un traitement particulier des pixels (resp. voxels) du
bord de l’image, nous considérons que l’image est imbriquée dans une
région infinie R0 contenant l’ensemble
des pixels (resp. voxels) du complémentaire de l’image. Par
définition, l’ensemble des régions est une partition des pixels
(resp. voxels) de l’image car chaque pixel (resp. voxel) appartient
exactement à une seule région de l’image.
La notion d’adjacence est étendue aux régions : deux régions A et
B sont α-adjacentes s’il existe un pixel a ∈ A
(resp. voxel) et un pixel b ∈ B (resp. voxel) tel que a et b
soient α-adjacents. Avec cette notion d’adjacence entre les
régions, les notions de α-chemin et de composante
α-connexe s’étendent directement aux régions. De plus, l’ordre
lexicographique sur les pixels (resp. voxels) s’étend également
directement aux régions en utilisant l’ordre sur le plus petit élément
de chaque région.
[a
]

[b
]

| Figure 4.1: Exemple de paradoxes topologiques arrivant lorsque la
connexité considérée est la même pour l’objet et pour son
complémentaire. (a) Une 8-courbe fermée en gris dont le
complémentaire est une seule composante 8-connexe. (b) Une
4-courbe fermée en gris dont le complémentaire est formée de
trois composantes 4-connexes : l’extérieur et «deux
intérieurs» : la première composante 4-connexe intérieure
est composée du pixel 1 et la seconde est composée du pixel 2. |
De nombreux travaux ont porté sur l’étude des problèmes topologiques
dans un espace discret
[HW83, Kov84, KR89, Kov89, KKM90a, KKM91, KU92].
En effet, l’utilisation d’une même relation d’adjacence pour un objet
et son complémentaire entraîne des paradoxes topologiques, comme ceux
présentés en 2D sur la Fig. 4.1. Ces problèmes sont
liés au théorème de Jordan
qui dit que dans ℝ2 le complémentaire de toute courbe fermée
simple est formée exactement de deux composantes connexes distinctes :
un extérieur et un intérieur. Ce théorème est l’un des piliers de la
topologie du plan. Dans le plan, toute courbe de
Jordan est homéomorphe au cercle unité
S2. Dans ℝ3, la notion équivalente est celle de
surface de Jordan
qui est une surface fermée simple.
La résolution des problèmes topologiques dans un espace discret se
fait en considérant une connexité différente pour l’objet et pour son
complémentaire [Udu94, Kon02, EL03]. En 2D, le couple de
connexité choisi (α, β) doit être tel que chaque
α-courbe fermée doit séparer ℤ2 en deux composantes
β-connexes. Un tel couple de connexité est appelé paire de
Jordan.
C’est le cas par exemple des couples (4,8) ou (8,4). En 3D, les
couples de connexités à utiliser sont par exemple (6,18) et
(6,26).
L’utilisation de ces couples de connexité va également intervenir dans
la définition de la relation d’imbrication entre régions.
Intuitivement, une région Ri est dite imbriquée2 dans une autre région
Rj si Rj «entoure» complètement Ri. Cette notion est
une relation topologique liée à la notion d’intérieur et d’extérieur
du théorème de Jordan. De ce fait, comme les régions sont définies
avec une seule connexité (4 en 2D, 6 en 3D), la connexité possible
pour le complémentaire est limitée à 8 en 2D et 18 ou 26 en 3D.
Définition 60 (imbrication)
Une région 2D (resp. 3D)
Ri est
imbriquée
dans une région Rj si et seulement si tout
chemin 8-connexe (resp. 18-connexe) allant d’un pixel
(resp. voxel) de Ri vers un pixel (resp. voxel) de R0 (la
région infinie) possède au moins un pixel (resp. voxel) appartenant
à la région Rj.
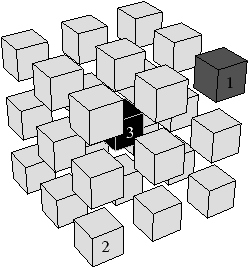
Sur l’exemple de la Fig. 4.1, la région 3,
composée des pixels noirs, n’est pas imbriquée dans la région 2 (la
région gris clair) car il existe un 8-chemin entre un pixel de la
région 3 et un pixel de la région infinie ne passant pas par la région
2. De ce fait, la région 3 est adjacente à une autre région que 2
appartenant à l’extérieur de 2 (même si dans ce cas cette zone de
contact est limitée à un point). En 3D, le chemin doit être
18-connexe (et non 26-connexe) à cause de la propriété de
quasi-variété des cartes combinatoires (cf. Def. 5
page ??). En effet, deux volumes d’une carte sont
nécessairement adjacents par une face. Lorsque deux voxels sont
18-adjacents mais pas 6-adjacents, il y a une seule arête entre les
voxels car le volume complémentaire est adjacent à ces deux voxels par
deux faces qui sont voisines. Par contre, lorsque deux voxels sont
26-adjacents mais pas 18-adjacents, comme c’est le cas pour le voxel
de la région 3 et le voxel de la région 1 dans la
Fig. 4.1, les deux voxels ne partagent pas
de sommet commun car les volumes ne partagent ni face, ni arête
commune. De ce fait, les frontières des régions 1 et 3 de l’exemple
sont disjointes et la région 3 touche uniquement la région 2 : la
région 3 est donc imbriquée dans la région 2 ce qui fait que la seule
connexité possible pour le complémentaire est la 18-connexité.
[a
]

[b
]
[c
]
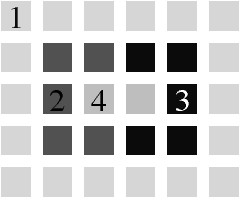
| Figure 4.2: Exemples de relation d’imbrication et de relation
d’imbrication directe. (a) La région 3 (pixels noirs) n’est pas
imbriquée dans la région 2 (pixels gris clair) car elle est
8-adjacente à la région 1. (b) La région 3 (voxels noirs) est
imbriquée dans la région 2 (voxels gris clair) car chaque
18-chemin entre la région 3 et la région infinie traverse la
région 2. (c) La région 4 est directement imbriquée dans la
région 1 bien que les régions ne soient pas adjacentes, car les
trois régions 2, 3 et 4 appartiennent à la même composante
8-connexe imbriquée dans 1. |
Il est simple de prouver que la relation d’imbrication est une
relation d’ordre. Il est souvent suffisant de s’intéresser à la
réduction transitive de la relation d’ordre afin de s’intéresser à la
plus petite région contenant une région donnée : c’est la relation
d’imbrication directe. Chaque région
Ri (à l’exception de la région infinie) est directement imbriquée
dans exactement une région Rj, Ri et Rj n’étant pas
nécessairement adjacentes (cf. l’exemple de la
Fig. 4.1). Par contre, chaque région possède
entre 0 et k régions directement imbriquées. Dans la suite de ce
manuscrit, nous utiliserons toujours la relation d’imbrication directe
que nous appellerons imbrication pour simplifier.
De nombreux travaux ont porté sur la représentation des contours dans
une image discrète
[Kov89, KR89, KKM90b, KKM91, Fio95]. Ces
travaux utilisent tous la notion de topologie
interpixel en 2D ou
intervoxel en 3D. Le principe intuitif de ces
topologies est de ne pas considérer uniquement les éléments de l’image
mais également tous les éléments de dimension inférieure séparant ces
éléments. Par exemple en 2D, les pixels (éléments unitaires 2D) sont
séparés par des lignels (éléments unitaires 1D),
eux-mêmes séparés par des pointels (éléments
unitaires 0D). En 3D, le principe est similaire en considérant les
voxels (éléments unitaires 3D),
surfels (éléments unitaires 2D), lignels et
pointels (cf. exemple Fig. 4.3). Plus formellement, la
notion de complexe cellulaire3 ℂn
[Kov89] est la décomposition cellulaire de l’espace
euclidien ℝn en grille régulière. Les notions d’adjacence et
d’incidence se retrouvent dans ℂn directement à partir des
notions de bord existantes dans
ℝn. ℂin est
l’ensemble des i-cellules de la décomposition cellulaire, et donc
ℂn=∪i=0n ℂin.
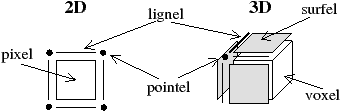
| Figure 4.3: Éléments interpixel et intervoxel. |
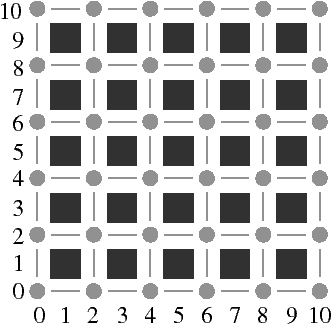
| Figure 4.4: Topologie de Khalimsky. |
Une autre manière d’introduire l’interpixel/intervoxel
[KKM90b] est l’utilisation de la topologie produit. Tout
d’abord, la topologie sur ℤ est définie en prenant tous les
nombres pairs comme des fermés, et les nombres impairs comme des
ouverts. Intuitivement, les fermés sont les pointels et les ouverts
les lignels. Cette topologie est appelée topologie de
Khalimsky ou topologie
digitale. Elle s’étend ensuite
directement en dimension n en effectuant le produit de n
topologies de Khalimsky 1D (cf. l’exemple en 2D donné
Fig. 4.4). Les ouverts sont les points ayant des
coordonnées toutes impaires, et les fermés les points ayant des
coordonnées toutes paires. Les autres points ayant les deux types de
coordonnées sont des points mixtes. Il a été prouvé dans
[KKM90b, KKM91] que la topologie de Khalimsky est
équivalente à la topologie des complexes cellulaires. De plus, le lien
entre les inter-éléments et la topologie produit de n ensembles
d’entiers fournit un codage simple des inter-éléments
[Lac03, KR04].
En 2D, la topologie de Khalimsky est donc la topologie produit ℤ
× ℤ, où les ouverts sont les pixels, les fermés les
pointels, et les lignels des points mixtes. En 3D, c’est ℤ ×
ℤ × ℤ avec les voxels étant les ouverts, les pointels
les fermés, et les lignels et les surfels des points mixtes. Avec ces
notations, deux inter-éléments sont incidents si la différence deux à
deux entre chaque coordonnée est au plus un, et ils sont adjacents
s’ils ont toutes leurs coordonnées égales sauf une, et si la
différence pour cette coordonnée est deux (intuitivement les deux
inter-éléments sont séparés par un inter-élément ce qui explique la
différence de deux).
Il est possible de définir la notion de chemin et de connexité pour un
ensemble d’inter-éléments de même dimension, de manière similaire aux
définitions pour les pixels et voxels. Nous utilisons par exemple un
chemin de surfels qui est défini par une suite de surfels (s1,
…, sk) tel que chaque couple de surfels consécutifs si,
si+1 soient adjacents.
Comme nous voyons dans la Def. 61 (que l’on peut
trouver par exemple dans [Her98, Kov08]), un des
avantages des approches inter-éléments est de pouvoir définir la
frontière entre deux régions par un ensemble d’éléments entre les
pixels (ou voxels) de la région et non pas par un ensemble de pixels
(ou voxels) ce qui pose des problèmes de non-symétrie. En effet, les
pixels (ou voxels) de la frontière entre deux régions A et B sont
pris soit dans la région A, soit dans la région B. Rendre cette
notion de frontière symétrique est possible en prenant à la fois les
pixels (ou voxels) dans A et dans B, mais cela pose alors un autre
problème qui est que la frontière n’est plus mince (c-à-d les
éléments de la frontière ne sont plus voisins d’éléments appartenant à
A et à B). Un autre avantage de la définition des frontières
inter-éléments est de permettre la définition de l’analogue du
théorème de Jordan dans le cas discret. Cela permet de prouver que
toute frontière sépare l’espace discret en deux composantes connexes.
Ce type d’approche a été utilisé afin de définir les surfaces en
intervoxels [Her98, Kov08]. Il faut noter que l’approche
[Her98] n’utilise pas directement une approche inter-éléments
mais utilise une approche à base de graphe, où les sommets du graphe
correspondent aux voxels et les arêtes représentent la relation
d’adjacence utilisée (par exemple la 6-adjacence). En pratique, si
l’adjacence utilisée est la 6-adjacence, ce graphe peut être vu comme
une représentation intervoxel ou chaque arête correspond à un surfel,
et les deux approches sont alors équivalentes.
La Def. 61 introduit la définition de frontière d’une
région en 2D et 3D en utilisant un espace interpixels/intervoxels.
Définition 61 (frontière)
Soit une région 2D
(resp. 3D), R. La frontière
de R est l’ensemble des lignels
(resp. surfels) incidents à un pixel (resp. voxel) de R et un pixel
(resp. voxel) n’appartenant pas à R.
Dans [Her98, Kov08], il est prouvé que ces frontières
ont des «bonnes» propriétés lorsque le couple de connexité
considéré est une paire de Jordan (ce qui est notre cas). En 2D,
chaque composante connexe de la frontière est courbe de Jordan. En
3D, chaque composante connexe de la frontière est une surface
presque-Jordan, c’est-à-dire qu’elle sépare l’espace en deux
parties disjointes : un intérieur et un extérieur.
Le terme presque-Jordan (défini dans [Her98]) est
employé car ces surfaces discrètes séparent bien l’espace en deux
composantes connexes, comme les surfaces de Jordan dans l’espace
euclidien, mais ce ne sont pas forcément des 2-variétés (cf. exemple
Fig. 4.5).
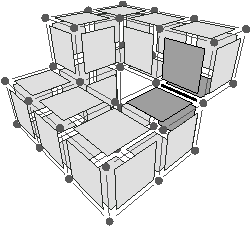
| Figure 4.5: Exemple de surface presque-Jordan qui n’est pas
une 2-variété. Le voisinage du lignel noir et épais est composé
des quatre surfels en gris foncé et n’est pas homéomorphe à une
2-boule ouverte. |
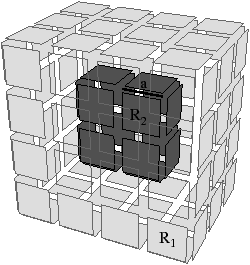
| Figure 4.6: Exemple de frontière non-connexe. La frontière de R1 est
composée de deux composante connexes de surfels car R1 possède
une cavité. |
Il faut noter que la frontière d’une région n’est pas forcément
connexe, lorsqu’une région possède des cavités (cf. exemple
Fig. 4.6). Dans ce cas, chaque frontière sépare la région
et une composante connexe de son complémentaire. Pour pouvoir
désigner plus précisément certaines parties de la frontière d’une
région, nous la décomposons en sous-parties en introduisant les
notions suivantes :
-
une arête/face frontière entre deux régions : c’est une
zone maximale de contact entre deux régions ;
- une courbe/surface frontière d’une région : c’est une
composante connexe de la frontière.
La notion d’arête/de face frontière (cf. Def. 62)
est importante car nous souhaitons représenter la multi-adjacence
inter-régions. Il faut donc savoir combien de fois deux régions se
touchent et pour cela être capable d’identifier précisément une zone
maximale de contact.
Définition 62 (arête/face frontière)
Une arête frontière
(resp. face frontière
) entre deux
régions A et B 2D (resp. 3D) est un ensemble maximal de lignels
(resp. surfels) E séparant un pixel (resp. voxel) de A et un
pixel (resp. voxel) de B vérifiant : pour chaque couple e1 et
e2 d’éléments de E, il existe un chemin d’éléments de E entre
e1 et e2 tel que chaque couple consécutif d’éléments du chemin
soit séparé par un pointel (resp. lignel) incident exactement à ces
deux éléments de E.
De manière intuitive, une arête/face frontière est un ensemble maximal
et connexe d’éléments séparant les deux régions A et B, tel qu’il
existe un chemin reliant tout couple d’éléments de cet ensemble.
C’est l’existence ou non de ce chemin qui fait que deux éléments
séparant A et B appartiennent à la même zone de contact ou pas.
La notion de surface frontière (cf. Def. 63)
est quant à elle nécessaire pour traiter correctement le cas des
régions ayant des cavités.
Définition 63 (courbe/surface frontière)
Une courbe (resp. surface) frontière d’une région R 2D (resp. 3D)
est une composante connexe de lignels (resp. surfels) appartenant à
la frontière de R.
En 2D, chaque région R possède toujours une courbe frontière dite
externe telle que l’intérieur de cette courbe contiennent tout les
pixels de R, et entre 0 et k contours internes, un par cavité
de R. Il en est de même en 3D pour la surface frontière externe et
les éventuelles surfaces frontières internes. La frontière entre deux
régions peut être vide lorsque les régions ne sont pas adjacentes,
elle peut être composée d’une seule arête/face frontière lorsque les
deux régions sont simplement adjacentes, ou de plusieurs arêtes/faces
frontières lorsque les régions sont multi-adjacentes.
Il est facile de prouver que les arêtes (resp. faces) frontières
forment une partition des courbes (resp. surfaces) frontières
c’est-à-dire qu’une courbe (resp. surface) frontière est une union
d’arêtes (resp. de faces) frontières, et que l’intersection de deux
arêtes (resp. faces) frontières différentes est toujours vide. De
même, les courbes (resp. surfaces) frontières forment une partition
des frontières. De ce fait, la frontière d’une région R est l’union
de toutes ses arêtes (resp. faces) frontières avec toutes les autres
régions.
4.2 Les Modèles Existants
4.2.1 Le Graphe d’Adjacence de Régions
La première structure de données qui a été définie dans l’objectif de
représenter une image segmentée est le graphe d’adjacence de
régions (appelé RAG)
[Ros74]. C’est un graphe associant un sommet à chaque
région de l’image, et deux sommets sont reliés par une arête lorsque
les deux régions correspondantes sont voisines.
[a
]
[b
]
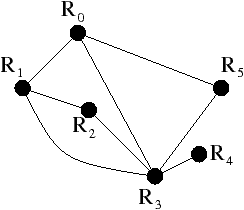
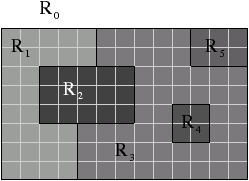
| Figure 4.7: Exemple de graphe d’adjacence des régions. (a) Une image
2D segmentée en régions. (b) Le RAG correspondant. |
Ce graphe d’adjacence possède comme avantages d’avoir une définition
simple et générique quelle que soit la dimension de l’image. Par contre,
il possède comme inconvénients majeurs de ne pas représenter les
adjacences multiples ni l’ordre entre les régions adjacentes à une
même région, de ne pas différencier les relations d’adjacence et les
relations d’imbrication, et de ne pas représenter toutes les cellules
ni les relations d’incidence. Ces problèmes deviennent majeurs dès la
dimension trois où le graphe d’adjacence contient alors très peu
d’information topologique.
4.2.2 Les Graphes Duaux
Pour résoudre ces problèmes, les graphes d’adjacences ont été étendus,
tout d’abord de manière directe pour représenter la
multi-adjacence, puis pour représenter l’ordre des régions autour
d’une région. Pour cela, les graphes duaux
ont été définis [WK94, KM95, Kro95].
L’idée principale des graphes duaux est de conserver deux graphes en
parallèle, un multi-RAG d’un côté, et son graphe dual de l’autre. Le
premier graphe représente les adjacences entre régions, avec des
boucles lorsqu’une région contient des régions imbriquées. Ces
boucles proviennent du fait que le graphe primal et son dual doivent
tous deux être connexes. De ce fait, dans le dual, une arête permet à
la région imbriquée d’être reliée à la région qui l’entoure. Cette
arête devient, dans le graphe primal, une boucle autour de la région
imbriquée.
[a
]
[b
]
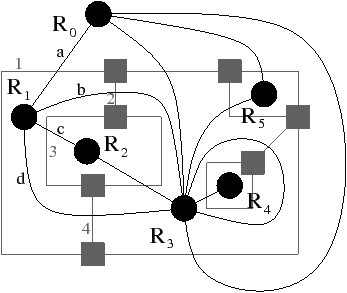
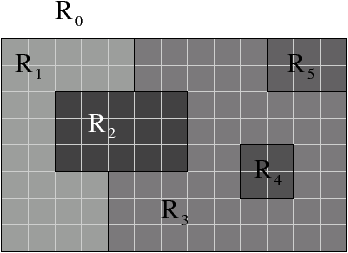
| Figure 4.8: Exemple de graphes duaux. (a) Une image 2d segmentée en
régions. (b) Les graphes duaux correspondant. En noir le graphe
primal (qui est un multi-RAG), et en gris son graphe dual. |
En parcourant simultanément les deux graphes, il est possible de
retrouver l’ordre des régions adjacentes à une région donnée. Sur
l’exemple de la Fig. 4.8, le parcours des régions
adjacentes à la région R1 de manière ordonnée se fait en partant
d’une arête d’extrémité R1 et de son arête duale, par exemple
(a,1). Ensuite, parmi les arêtes d’extrémité R1 (b, c et
d), il en existe seulement deux ayant leur arête duale adjacente à
l’arête 1. Ces deux arêtes sont les deux orientations possibles pour
tourner autour de la région R1. Nous choisissons un couple, par
exemple (b,2) et continuons le parcours en prenant parmi les arêtes
incidentes à R1 celle telle que son arête duale soit adjacente à
l’arête 2. Il y a encore deux possibilités, mais une des deux est
l’arête précédente du parcours. Nous choisissons donc l’autre qui est
(c,3). La dernière arête obtenue est (d,4) avant de revenir sur
l’arête initiale (a,1).
Les graphes duaux résolvent certains problèmes du RAG. En effet, leurs
principaux avantages sont qu’ils :
-
représentent les adjacences multiples et les imbrications ;
- représentent toutes les cellules de l’image : les faces et les
arêtes dans le graphe primal, et les arêtes et les sommets dans le
graphe dual.
Mais il reste des inconvénients :
-
il faut maintenir en parallèle deux graphes, ce qui complique et
multiplie par deux les mises à jour ;
- il faut analyser la géométrie des arêtes afin de reconnaître la
relation d’imbrication, en trouvant quels sommets sont entourés
géométriquement par une boucle (il faut alors associer ou retrouver
la géométrie des arêtes frontières à chaque arête du graphe) ;
- ce modèle semble très difficilement extensible en dimension
supérieure. En effet, en nD, seules les n et (n−1)-cellules
seraient représentées dans le graphe, et les 0 et 1-cellules dans le
dual.
C’est pour répondre à ces problèmes que les travaux cherchant à
utiliser les cartes combinatoires pour représenter des images se sont
développés. En effet, une carte combinatoire 2D code explicitement
l’ordre des arêtes autour des sommets, et représente toutes les
cellules de la subdivision (sommets, arêtes et faces). Le principe des
deux approches principales développées durant les thèses de
Jean-Philippe Domenger, Luc Brun et Christophe Fiorio est d’utiliser
une carte combinatoire pour représenter les frontières interpixels des
régions de l’image. Les deux approches sont similaires sur la
définition de la carte combinatoire utilisée, mais diffèrent pour le
codage de la carte, le codage de la relation d’imbrication et pour
l’algorithme calculant le modèle à partir de l’image.
4.2.3 Les Cartes Discrètes
Le premier modèle, appelé carte discrète,
a été développé initialement durant la thèse de Jean-Philippe Domenger
puis durant la thèse de Luc Brun (cf. exemple
Fig. 4.2.3). Ce modèle utilise une carte combinatoire
M=(B,α,σ) dans laquelle chaque arête correspond à une
arête frontière entre deux régions de l’image, et chaque sommet
correspond soit à l’intersection de plus de deux arêtes frontières
(donc 3 ou 4 frontières vu que l’espace sous-jacent est discret), soit
à un sommet arbitraire de l’arête frontière dans le cas d’une arête
frontière fermée (cas de la frontière entre les régions R3 et R4
sur l’exemple). Chaque face (c’est-à-dire une orbite ⟨ϕ⟩)
est identifiée par une étiquette, et λ donne pour chaque brin
l’étiquette de sa face (ces faces sont numérotées de f1 à f7 sur
l’exemple de la Fig. 4.2.3). La face représentant
l’extérieur de la carte combinatoire est appelée face
infinie (la face f1 de l’exemple) tandis que
les autres faces sont appelées faces finies. Par convention, les brins
sont numérotés de telle manière que pour chaque brin b de numéro
i, le brin α(b) soit numéroté −i. Cette convention permet,
lorsque les brins sont représentés dans un tableau, de ne pas avoir
besoin de représenter explicitement l’involution α. Par contre,
cela complexifie les mises à jour lorsqu’il faut modifier cette
involution, car cela nécessite de réorganiser les brins au sein du
tableau.
[a
]
[b
]
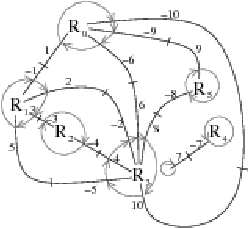
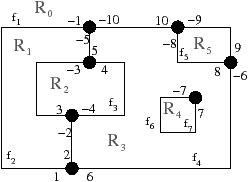
| Figure 4.9: (a) La carte discrète et (b) le graphe topologique des
frontières de l’image de la Fig. 4.2.2. Les
brins des deux modèles sont numérotés de manière identique
pour faciliter la comparaison. |
De par sa définition, lorsqu’une région est imbriquée dans une autre
région (comme la région R4 dans l’exemple de la
Fig. 4.2.3), la carte combinatoire n’est pas
connexe. En effet, il n’y a pas d’arête frontière reliant les deux
courbes frontières représentant l’extérieur de la face et la cavité.
Dans ce cas, la carte est composée d’un ensemble de composantes
connexes, chacune ayant une face infinie (sur l’exemple de la
Fig. 4.2.3, il y a deux composantes connexes donc deux
faces infinies f1 et f6). Il n’existe pas de relation dans la
carte combinatoire entre les différentes composantes
connexes4. Pour résoudre ce problème, les
relations d’imbrication sont représentées à l’aide de deux fonctions
sur les étiquettes des faces : Parent et Children.
La fonction Parent associe à chaque face infinie l’étiquette
de la face finie la contenant (à l’exception de la face infinie
englobant l’image qui n’est contenue dans aucune face). La fonction
Children associe à chaque face finie l’ensemble des
étiquettes des faces infinies imbriquées dans la face (par exemple
Parent(f6)=f4 et Children(f4)={f6}). Ces
deux fonctions permettent de parcourir l’ensemble des courbes
frontières d’une région donnée, et permettent également de retrouver
la région entourant une autre région. Enfin, la géométrie de la carte
discrète est codée à l’aide d’une matrice d’éléments interpixels dans
laquelle seuls les pointels associés aux sommets, et seuls les lignels
appartenant aux frontières sont allumés. Chaque brin est associé avec
un couple (pointel, lignel) donnant le point de départ et la direction
initiale de l’arête frontière. À partir de ce point de départ, il est
simple de parcourir tous les lignels de l’arête frontière en suivant
les lignels allumés jusqu’à trouver un pointel allumé indiquant la fin
de l’arête frontière.
Les cartes discrètes ont été ensuite étendues en 3D
[BDDW99, BDD01, Des01, BDDV03] en
utilisant un principe similaire à la solution proposée en 2D. Les
principaux changements sont l’utilisation d’une carte combinatoire 3D
codée par une matrice d’éléments intervoxels, et représentant les
régions. Un brin est donc représenté par un triplet (pointel, lignel,
surfel), et des fonctions sont définies sur ces triplets pour
retrouver directement les différentes relations sur les brins. Mais
cette solution n’a pas pu être utilisée en pratique car car la
représentation des brins par un triplet n’est possible que pour
des images étiquetées dites faiblement bien-composées, c’est à
dire dans lesquelles il n’existe pas deux voxels 18-adjacents
appartenant à la même région. Cela rend ce modèle peu utilisable en
pratique, car il nécessite une étape de normalisation d’une image
avant de pouvoir en calculer la carte discrète, étape itérative et
donc coûteuse, qui de plus modifie les régions de l’image
segmentée. Cela rend également difficile les opérations puisqu’après
chaque modification de la carte, il faut vérifier si cela n’a pas
entraîné une configuration interdite, et le cas échéant régler le
problème, à nouveau de manière itérative. Pour ces raisons, autant
l’approche 2D a été utilisée afin de résoudre des problématiques de
segmentation d’images [BDB97, BD97, BB98, BDM03],
autant le problème lié à l’approche 3D c’est avéré bloquant. De ce
fait, les travaux successeurs de cette approche ont consisté à
repartir sur un modèle à base de graphe d’adjacence étendu, en le
liant avec une matrice d’éléments intervoxels
[BBDD08, Bal09, BBD09].
4.2.4 Le Graphe Topologique des Frontières
Le second modèle, appelé graphe topologique des
frontières
(TGF), a été développé durant la thèse de Christophe
Fiorio (cf. exemple Fig. 4.2.3). Son principe,
très proche de la carte discrète, est toujours d’utiliser une carte
combinatoire représentant une arête par arête frontière entre
deux régions de l’image. Les différences portent simplement sur :
-
la carte utilisée qui est la carte duale de celle utilisée dans
les cartes discrètes (cf. Section 2.2.2) ;
- le codage des relations d’imbrication : chaque région possède
une liste de brins, un par courbe frontière. Le premier brin est un
brin de la courbe frontière externe, les éventuels brins suivants
appartiennent à des courbes internes.
La carte combinatoire et les régions sont liées car chaque brin
connaît sa région d’appartenance. Enfin, une région supplémentaire (la
région infinie) est ajoutée qui représente le complémentaire de
l’image.
La première différence est anecdotique car les utilisations d’une
carte ou de sa duale sont équivalentes. La seconde différence change
la manière de parcourir la structure. Ici, la notion de région est
maintenant explicitée contrairement aux cartes discrètes. De ce fait,
retrouver les courbes frontières internes d’une région se fait ici à
l’aide de la liste des brins, ce qui est équivalent à l’utilisation de
la fonction Children pour les cartes discrètes. Enfin, une
dernière différence entre les deux modèles concerne la manière usuelle
de les dessiner, comme nous pouvons le vérifier sur la
Fig. 4.9. Pour les cartes discrètes, les arêtes sont
dessinées le long des frontières des régions ce qui permet de faire
plus facilement le lien avec la géométrie des régions, alors que pour
le TGF les arêtes sont dessinées de manière similaire à un RAG ce qui
rend son interprétation visuelle plus délicate. Mais la encore, c’est
une différence négligeable, d’autant plus que c’est uniquement une
habitude et qu’il est possible de dessiner le TGF de manière similaire
aux cartes discrètes (comme nous l’avons présenté
Section 2.2.2).
Lorsque j’ai débuté ma thèse, l’objectif était d’étendre ces modèles
en 3D. Les cartes combinatoires avaient déjà été définies en dimension
quelconque, il semblait alors naturel de vouloir poursuivre les
travaux autour de la carte discrète ou du TGF afin d’utiliser ces
cartes combinatoires pour représenter des images 3D. Mais cette tâche
s’est vite avérée très difficile de par la définition directe de ces
deux modèles. En effet, le problème en 2D est suffisamment simple pour
que nous puissions définir directement la subdivision voulue
(principalement une arête par arête frontière) et la carte associée
(car une arête est toujours composée de deux brins dans une carte
combinatoire 2D fermée). Cela devient beaucoup plus délicat en 3D où
il faut définir la notion de surface frontière en intervoxel, mais
cette notion n’est plus suffisante car nous devons nous intéresser aux
bords de ces surfaces et à la manière dont ils se rejoignent. Les cas
possibles deviennent beaucoup plus nombreux et complexes à
visualiser. Enfin, le nombre de brins associés aux cellules de la
subdivision peut maintenant être quelconque ce qui complexifie encore
plus la tâche.
Pour résoudre ce problème, je me suis reposé la question de la
définition d’un modèle 2D mais dans l’optique d’avoir une définition
pouvant s’étendre directement en dimension supérieure. C’est ce qui
m’a amené à définir la carte topologique,
qui en 2D est très proche des deux modèles
qui existaient déjà, mais dont l’avantage principal est sa définition
progressive basée sur la notion nouvelle de niveaux de
simplification. Ces niveaux
facilitent la définition du modèle, sont directement extensibles en
dimension supérieure, fournissent directement un algorithme de
construction et enfin facilitent l’étude des propriétés. En effet, un
niveau de simplification s’obtient à partir du niveau précédent par
application d’un seul type d’opération, ce qui simplifie l’étude des
propriétés en diminuant le nombre de cas à considérer. Une version
préliminaire de ces travaux a été présentée dans
[BDF00, BDF01], un résumé dans [DB07], et
les versions complètes ont été publiées en 2D dans [DBF04]
et en 3D dans [Dam08].
4.3 Carte Topologique 2D
Pour définir la carte topologique 2D, c-à-d la carte
combinatoire minimale décrivant une image 2D étiquetée, nous avons
défini la notion de niveaux de simplification. Le principe
général de ces niveaux de simplification consiste à donner une suite
de définitions constructive de chaque niveau à partir du niveau
précédent. Chaque niveau s’obtient à partir du niveau précédent par
application d’un ensemble d’opérations de suppression de même type.
Définir la carte topologique revient donc à définir le niveau initial,
puis les propriétés des cellules à supprimer pour chaque nouveau
niveau.
Pour décrire une image étiquetée, la carte initiale va représenter
chaque élément interpixel de l’image, le premier niveau va supprimer
les arêtes séparant deux pixels de même étiquette, et le dernier niveau
va supprimer les sommets se trouvant au milieu d’une arête
frontière. Ces niveaux sont définis plus formellement par les
Defs. 64, 65 et 66.
La carte combinatoire initiale C=(B,β1,β2), appelée
niveau 0, représente chaque élément interpixel de l’image
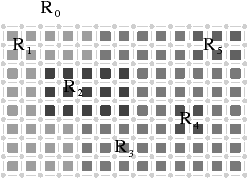
(cf. Fig. 4.10). Cette carte contient (n × m)+1
faces, et ne représente pas les frontières des régions mais tous les
éléments de l’image.
Définition 64 (carte de niveau 0)
La carte de niveau 0
correspondant à une image étiquetée de n
× m pixels est la carte combinatoire ayant n × m faces
carrées, 2-cousues entres elles lorsqu’elles sont adjacentes,
chacune de ces faces représentant un pixel de l’image, plus une face
englobante représentant la région infinie.
[a
]
[b
]
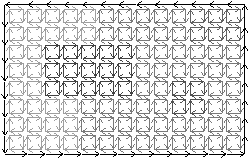
| Figure 4.10: Le niveau 0 d’une image 2D. (a) Une image
étiquetée. (b) La carte de niveau 0 correspondante. |
4.3.1 Le Niveau 1
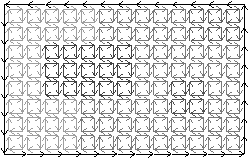
La carte de niveau 1 s’obtient en supprimant toute les arêtes séparant
deux pixels de même étiquette (cf. Fig. 4.11). Après ces
suppressions, les seules arêtes restantes séparent deux régions
distinctes : cette carte représente donc les frontières interpixels
des régions de l’image. C’est uniquement lors de la construction de ce
niveau que les données de l’image sont prises en compte afin de décrire
les régions de l’image.
Définition 65 (carte de niveau 1)
La carte de niveau 1
est la
carte obtenue à partir de la carte de niveau 0 en supprimant chaque
arête séparant deux pixels de même étiquette.
[a
]
[b
]
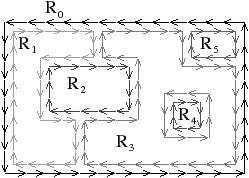
| Figure 4.11: La carte de niveau 1 d’une image. (a) Le niveau 0.
(b) La carte de niveau 1 correspondante. |
La dernière étape de simplification utilise uniquement la carte
combinatoire et les propriétés des cellules.
4.3.2 Le Niveau 2
La carte de niveau 2 s’obtient en supprimant successivement tous les
sommets supprimables et de degré deux de la carte du niveau précédent
(cf. Fig. 4.12). En effet, ces sommets appartiennent
nécessairement au milieu d’une même arête frontière puisque, comme
nous l’avons vu lors de la présentation des modèles existants
Section 4.2.3, les sommets extrémités de ces frontières
sont nécessairement soit incidents à une boucle (donc de degré un),
soit de degré trois ou quatre.
[a
]
[b
]
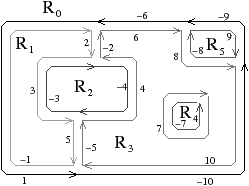
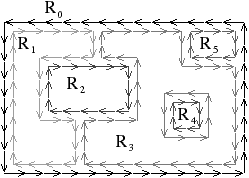
| Figure 4.12: La carte de niveau 2 d’une image. (a) Le niveau 1.
(b) La carte de niveau 2 correspondante. La numérotation des
brins utilisée ici est la même que pour la
Fig. 4.9 pour faciliter la comparaison. |
Définition 66 (carte de niveau 2)
La carte de niveau 2
est la carte
obtenue à partir de la carte de niveau 1 en supprimant
successivement chaque sommet supprimable et de degré deux.
Dans cette définition, il est nécessaire d’utiliser les deux
conditions supprimable et de degré deux, pour résoudre correctement
le cas des boucles (dans le cas général, si le sommet est incident à
deux arêtes distinctes, il est de degré deux et supprimable). Deux cas
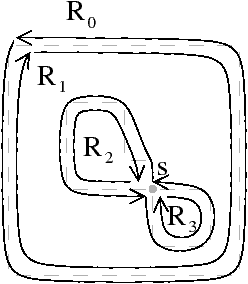
peuvent se produire. Premièrement, lorsque deux boucles sont
incidentes au même sommet (cf. Fig. 4.3.2), le sommet
est de degré deux (incident à exactement deux arêtes distinctes), mais
il n’est pas supprimable. Le second cas est celui d’un sommet de degré
un (cf. Fig. 4.3.2). Ce type de sommet est supprimable
mais ne doit pas l’être sous peine de faire disparaître totalement
l’arête frontière associée à la boucle (l’arête frontière entre R1
et R2 sur l’exemple). Il n’y a pas d’autre cas à considérer que ces
deux cas de par les propriétés de l’espace discret sous-jacent qui
rend impossible plus de deux boucles autour d’un même sommet.
[a
]
[b
]
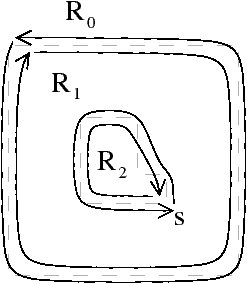
| Figure 4.13: Cas pour lesquels la Def. 66 utilise les
deux conditions : sommets supprimables et de degré deux. (a) Le
cas d’un sommet s de degré deux qui ne doit pas être supprimé
car il n’est pas supprimable. (b) Le cas d’un sommet s
supprimable qui ne doit pas être supprimé car il n’est pas de
degré deux. |
Il faut noter le terme successivement qui est nécessaire pour
traiter correctement le cas des arêtes frontières fermées (comme la
frontière entre R3 et R4 dans l’exemple). En effet, tous les
sommets de ce type de frontière sont initialement supprimables et de
degré deux. Si les suppressions se font de manière simultanée, tous
ces sommets vont être supprimés et l’arête frontière va
disparaître. Par contre, en effectuant les suppressions de manière
successive, le dernier sommet considéré sera alors de degré un
puisqu’il ne restera plus qu’une seule arête : de ce fait il sera
conservé. Il faut noter que la position de ce sommet dépend de l’ordre
de suppression des sommets, mais ce n’est pas important car
topologiquement toutes les configurations obtenues sont équivalentes.
4.3.3 La Carte Topologique
Cette carte de niveau 2 est équivalente aux deux modèles qui
existaient au préalable (la carte discrète et le graphe topologique
des frontières). La carte utilisée est la même que celle du TGF : la
permutation relie les arêtes frontières successives d’une même courbe
frontière contrairement à la carte discrète qui est la carte duale.
Comme dans ces deux modèles, nous devons rajouter des informations
afin de représenter les relations d’imbrication. Nous avons choisi de
les représenter par un arbre d’imbrication des régions contenant
chaque région de l’image. Pour lier les deux structures de données,
chaque brin b connaît sa région d’appartenance, notée
region(b), et chaque région connaît un de ses brins (qui
doit vérifier des propriétés spécifiques comme expliqué ci-dessous).
La racine de l’arbre d’imbrication est toujours la région
infinie. Chaque région R connaît la région dans laquelle elle est
directement imbriquée (notée father(R)). À l’inverse,
chaque région R connaît les régions qui sont directement imbriquées
dans R. Pour avoir un accès direct aux cavités de R, ces
régions sont regroupées par composantes 8-connexe. En effet, chaque
composante 8-connexe de régions directement imbriquée dans R
représente une même cavité (cf. exemple
Fig. 4.14). Cette définition respecte la contrainte,
déjà évoquée plus haut, que la connexité de l’objet doit être
différente de la connexité du fond [KR89]. Dans notre cas,
l’objet est la région considérée R qui est 4-connexe par
définition, et le fond est l’union de toute les autres régions qui
est donc considérée avec la 8-connexité.
De ce fait, une région R a pour fils l’ensemble des plus petites
régions (au sens lexicographique) de chaque composante 8-connexe de
régions imbriquées, les autres régions étant accessibles à partir de
ces régions par une relation d’appartenance à la même composante
connexe.
[a
]
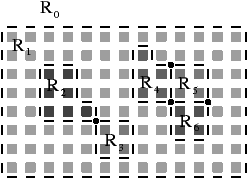
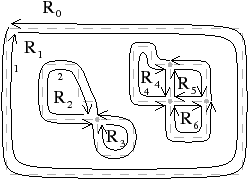
[b
]
[c
]
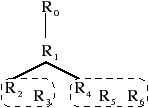
| Figure 4.14: Exemple d’arbre d’imbrication des régions. (a) Une image
2D étiquetée, ses régions, et ses frontières interpixels. (b) La
carte de niveau 2 correspondante. Cette carte est composée de
trois composantes connexes car la région R1 possède deux
cavités : une première composée des régions {R2,R3} et une
seconde des régions {R4,R5,R6}. (c) L’arbre d’imbrication
associé. R1 a pour fils R2 et R4 (les plus petites
régions de chaque composante 8-connexe de régions imbriquées),
les autres régions sont accessibles par la relation sameCC
symbolisée par les ensembles pointillés. |
Nous identifions un brin particulier de chaque région R appelé
brin représentant, noté
rep(R). Ce brin représentant doit vérifier la propriété :
region(β2(rep(R))<R (la région du brin
atteignable par β2 à partir du brin représentant doit être plus
petite que la région R). Cette propriété garantit que le brin
représentant est situé sur le contour frontière extérieur de la région
(car les régions imbriquées dans R sont forcément plus grandes que
R dans l’ordre lexicographique). De plus, cela garantit également
que pour chaque ensemble 8-connexe de régions, en prenant la plus
petite région de cet ensemble A, la région du brin
β2(rep(A)) est toujours la région dans laquelle A (et
donc toute les régions de la composante 8-connexe) est directement
imbriquée.
Dans la carte de la Fig. 4.3.3, le brin représentant
de R1 est forcément le brin 1 (car c’est le seul brin de R1
vérifiant la propriété ci-dessus). Le brin représentant de R2 est
le brin 2 et celui de R4 est le brin 4. Dans ces trois cas,
nous pouvons vérifier que le brin relié par β2 au brin
représentant appartient à la région dans laquelle est imbriquée la
région du brin (par exemple pour le brin 2 qui appartient à la
région R2, β2(2) appartient à la région R1 et R2 est
bien imbriquée dans R1).
Une région R est dite isolée lorsque
qu’elle est la seule région d’une composante 8-connexe. Une région de
ce type est imbriquée dans une région englobante et n’a pas d’autre
région adjacente sauf éventuellement des régions imbriquées (formant
des cavités et donc n’appartenant pas à la même composante 8-connexe).
L’arbre d’imbrication des régions et les propriétés sur le brin
représentant font qu’il est possible de parcourir directement chaque
courbe frontière d’une région R donnée : la courbe extérieure est
obtenue par l’orbite ⟨β1⟩(rep(R)), et ses
éventuelles courbes frontières intérieures s’obtiennent par les
orbites ⟨β1⟩(rep(β2(F)) pour chaque fils F de
R. De plus, l’ordre des régions et la position du brin représentant
se calculent sans surcoût lors du balayage de l’image pour construire
la carte [Dam08].
La carte combinatoire de niveau 2 plus l’arbre d’imbrication des
régions permet de représenter la topologie de l’image (les régions et
les cellules de la subdivision, les relations d’incidence,
d’adjacence et d’imbrication). Mais il faut également représenter la
géométrie des régions. Pour cela, nous pouvons utiliser la même
solution que celle des cartes discrètes, c’est-à-dire utiliser une
matrice d’éléments interpixels dans laquelle nous allumons les lignels
appartenant à une frontière interpixel et les pointels à
l’intersection de plus de deux arêtes frontières (cf. exemple
Fig. 4.3.3). Il suffit alors d’associer à chaque brin
un couple (pointel, lignel) pour donner le point de départ et la
direction de l’arête frontière associée pour être capable de retrouver
la géométrie de chaque élément en combinant les informations données
par la carte (par exemple pour retrouver toutes les courbes frontières
d’une région) et celles données par la matrice.
Nous avons expérimenté d’autres types de représentation de la
géométrie [Dam01, DBF04] dans lesquelles nous associons
des listes de points 2D à chaque arête orientée (cf. exemple
Fig. 4.15), ou une autre variante dans laquelle nous
associons également un point 2D à chaque sommet de la carte
(cf. exemple Fig. 4.16) ce qui évite de représenter
plusieurs fois les points extrémités des arêtes frontières. Il est
possible d’envisager d’autres solutions, par exemple en utilisant des
cartes généralisées 1D afin de s’affranchir de l’orientation, voire
d’associer des ensembles de pixels à chaque région…Chaque
méthode a ses propres avantages et inconvénients qui, de manière
classique, oscillent entre gain en espace mémoire et gain en temps
d’accès aux informations. La représentation par matrice d’éléments
interpixel est plus coûteuse en espace mémoire, mais facilite les
parcours, par exemple pour parcourir les pixels à l’intérieur d’une
région donnée. Les représentations de la géométrie des frontières
offrent une représentation plus compacte en mémoire, facilitent les
parcours de la géométrie des frontières qui est donnée explicitement,
mais rends plus complexe le parcours des pixels des régions qui ne sont
pas manipulables directement.
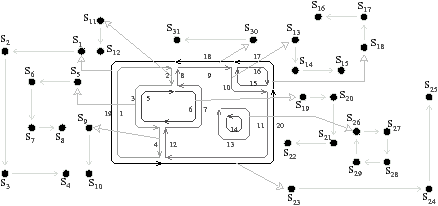
| Figure 4.15: Exemple de représentation de la géométrie en associant
une liste de points 2D à chaque arête orientée. Les sommets aux
extrémités des listes sont dupliqués entre toutes les listes des
arêtes incidentes aux mêmes sommets. |
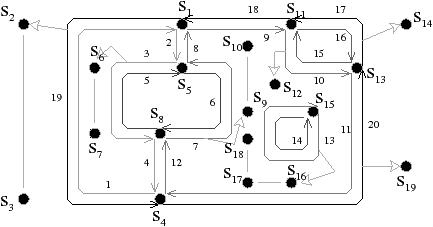
| Figure 4.16: Exemple de représentation de la géométrie en associant
une liste de points 2D à chaque arête orientée privée de ses
extrémités, et un point 2D à chaque sommet. Ces sommets ne sont
donc plus dupliqués. |
Nous appelons carte topologique le
modèle composé de la carte combinatoire de niveau 2, de l’arbre
d’imbrication des régions, et d’une représentation de la géométrie.
Ce modèle est équivalent aux deux modèles qui existaient déjà au
démarrage de mes travaux, mais nous pouvons observer dans les
différentes définitions des niveaux les avantages de notre approche
par simplifications successives. Les définitions sont simples car
progressives. Nous n’avons pas besoin de définir la notion d’arête
frontière mais simplement de nous intéresser aux éléments à supprimer
(par contre nous utilisons les arêtes frontières pour prouver les
propriétés des cartes topologiques). De plus, il est facile d’ajouter
des niveaux de simplification intermédiaires comme par exemple dans
[DBF04] où nous avions un niveau supplémentaire pour lequel
chaque arête correspondait à un ensemble de lignels alignés. Enfin, le
principal avantage de ces niveaux de simplification est de s’étendre
directement en dimension supérieure.
4.4 Carte Topologique 3D
Afin de définir la carte topologique 3D, nous appliquons le même
principe qu’en dimension 2 des niveaux de simplification. Nous
commençons par définir une carte combinatoire représentant chaque
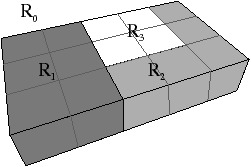
élément intervoxel de l’image (cf. Fig. 4.17) puis
nous la simplifions progressivement.
Définition 67 (carte de niveau 0)
La carte de niveau 0
correspondant à
une image étiquetée de n × m × l voxels, est la carte
combinatoire ayant n × m × l volumes cubiques,
3-cousus entre eux lorsqu’ils sont adjacents, chacun de ces
volumes représentant un voxel de l’image, plus un volume englobant
représentant la région infinie.
[a
]
[b
]
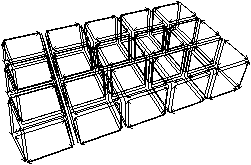
| Figure 4.17: Le niveau 0 d’une image 3D. (a) Une image
étiquetée. (b) La carte de niveau 0 correspondante (pour des
raisons de visibilité, nous ne dessinons pas de manière générale
le volume infini). |
4.4.1 Le Niveau 1
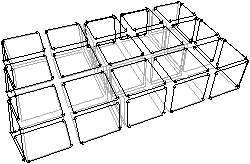
Le niveau 1 est totalement équivalent au niveau 1 en dimension 2 en
remplaçant pixel par voxel : il consiste à fusionner les voxels pour
représenter les frontières des régions
(cf. Fig. 4.18).
Définition 68 (carte de niveau 1)
La carte de niveau 1
est la
carte obtenue à partir de la carte de niveau 0 en supprimant chaque
face séparant deux voxels de même étiquette.
[a
]
[b
]
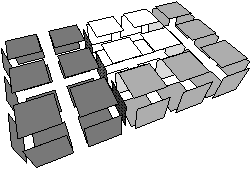
| Figure 4.18: Le niveau 1 d’une image 3D. (a) La carte de niveau 1
obtenue à partir de la carte de niveau 0 de la
Fig. 4.4. (b) La subdivision
correspondante. |
Cette carte de niveau 1 représente les frontières de chaque région. En
suivant le même principe que pour la dimension 2, nous allons
maintenant simplifier cette carte pour représenter chaque relation
d’adjacence de manière unique. Le fait d’avoir augmenté l’espace d’une
dimension entraîne de manière logique un niveau de simplification
supplémentaire : nous allons tout d’abord supprimer des arêtes puis
supprimer des sommets. Les suppressions doivent être réalisées par
dimensions décroissantes car la suppression d’une i-cellule diminue
le degré des (i−1)-cellules. De ce fait, une (i−1)-cellule peut
devenir supprimable après la suppression de i-cellules. Traiter les
cellules par dimensions décroissantes permet de garantir qu’à la fin
du traitement il ne reste plus de cellule supprimable.
4.4.2 Le Niveau 2
Pour définir le niveau 2, nous devons supprimer deux types d’arêtes :
les arêtes supprimables et de degré deux (de manière similaire au cas
de la dimension 2) et les arêtes pendantes.
Définition 69 (carte de niveau 2)
La carte de niveau 2
est la carte
obtenue à partir de la carte de niveau 1 en supprimant
successivement chaque arête supprimable qui est de degré deux ou
pendante.
Nous devons utiliser les deux conditions supprimable et de degré
deux, pour les mêmes raisons qu’en 2D : le cas d’une arête entre deux
faces repliées sur l’arête (cf. Fig. 4.4.2), et
le cas d’une région isolée
(cf. Fig. 4.4.2). Dans le premier exemple,
l’arête incidente à R2 et à R3 est conservée car elle est de
degré deux mais non supprimable. Dans le second exemple, la dernière
arête de la face de R2 est conservée car elle est de degré un et
n’est pas pendante (c’est une arête isolée). Dans ces deux cas, la
suppression de l’arête entraînerait la suppression d’une face (et même
de deux faces dans le premier cas) et donc la perte d’une relation
d’adjacence entre les deux régions incidentes à la face.
[a
]
[b
]
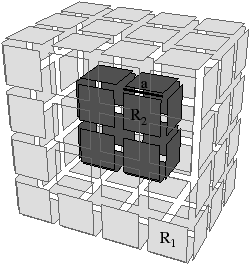
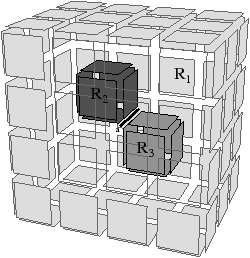
| Figure 4.19: Cas pour lesquels les deux conditions de la
Def. 69 sont nécessaires. (a) Le cas d’une arête
a de degré deux qui ne doit pas être supprimée car elle n’est
pas supprimable (cette configuration est obtenue en supprimant
toutes les autres arêtes incidente à R2 et R3 qui étaient
toutes supprimables et de degré deux ou pendantes). (b) Le cas
d’une arête a supprimable mais qui ne doit pas être supprimée
car elle n’est pas de degré deux (configuration obtenue en
supprimant toutes les autres arêtes incidentes à R2). L’arête
restante est n’importe quelle arête de la subdivision initiale
et dépend de l’ordre de traitement des arêtes. |
Mais il est nécessaire d’ajouter une condition pour supprimer les
arêtes pendantes. En effet, une arête de degré deux dans la carte de
niveau 1 peut devenir pendante après certaines suppressions d’arêtes
(cf. Fig. 4.20). Il faut noter que ce type de
cas ne se posait pas en dimension 2 car un sommet ne peut pas être
pendant.
[a
]
[b
]
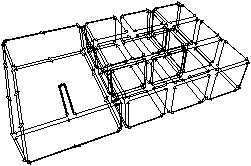
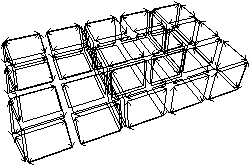
| Figure 4.20: Le niveau 2 d’une image 3D en cours de
construction. (a) La carte de niveau 1 de la
Fig. 4.18. (b) La carte de niveau 2 en cours
de construction. Certaines arêtes de degré deux ont été
supprimées. L’arête en gras était de degré deux dans la carte de
niveau 1 et est maintenant de degré un. |
Ne pas supprimer les arêtes de degré un (à l’exception des
arêtes pendantes) fait que nous n’allons pas supprimer une face
composée d’une seule arête (cas de la représentation minimale de la
sphère, comme pour la région R2 dans la
Fig. 4.4.2), ni supprimer une arête interne
à une face dont la suppression aurait pour conséquence que la face ne
soit plus homéomorphe à un disque (cf exemple
Fig. 4.21).
[a
]
[b
]
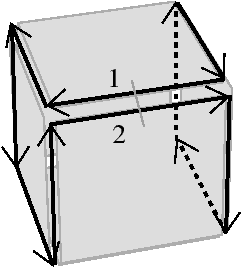
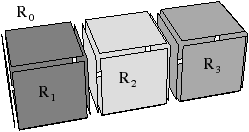
| Figure 4.21: Cas d’une arête de degré un non pendante. (a) Une
configuration composée de quatre régions, R0 étant la région
infinie englobant les trois autres régions. (b) La face séparant
R0 et R2 dans la carte de niveau 2 (en fait seule la
demi-face est dessinée, il faudrait représenter la même
demi-face du coté de R0). L’arête {1,2} est de degré un
mais n’est pas pendante. Cette arête doit être conservée pour
préserver la face homéomorphe à un disque, ou dit autrement afin
de ne pas déconnecter l’orbite face en deux. |
Les arêtes de degré un non pendantes sont appelées arêtes
fictives car contrairement
aux autres arêtes, elles ne représentent pas le bord d’une face
frontière entre deux régions. Par opposition, les autres arêtes sont
appelées arêtes réelles.
Pour supprimer toute les arêtes données par la
Def. 69, nous devons être capables de tester si une
arête est supprimable et de degré deux ou pendante.
Tester si une arête est supprimable se fait en testant pour un brin
b de l’arête si β23(d)=β32(d) (cf.
Def. 49). Si ce test est vrai pour un brin,
alors il est vérifié pour chaque brin de l’arête5 et l’arête
est supprimable par définition. Il faut alors tester si l’arête
correspond à un des deux cas de la Def. 49 :
une arête de degré deux, ou une arête pendante. L’arête est de degré
un si les deux brins b et β2(d) appartiennent à la même face,
c-à-d β2(d) ∈ ⟨β1⟩(d). Il est possible
d’effectuer ce test en parcourant l’orbite ⟨β1⟩(d) et en
vérifiant si le brin β2(d) est trouvé lors de ce parcours. Mais
la complexité de cette opération est linéaire en nombre de brins de la
face contenant l’arête. Comme ce test doit être fait pour chaque arête
de la carte, cela nous donne une complexité quadratique pour la
construction de la carte de niveau 2. Pour améliorer cette
complexité, nous utilisons les arbres union-find
[Tar75] qui permettent de manipuler efficacement des ensembles
disjoints.
Cette structure de données est manipulée à l’aide de deux primitives :
find qui retourne le représentant d’un élément donné, et
union qui fusionne deux ensembles. L’intérêt de cette structure
est que, en utilisant deux optimisations simples, la complexité
amortie d’un ensemble de m opérations union-find sur un
ensemble contenant n éléments est en O(n.α(m,n)) avec
α(m,n) étant l’inverse de la fonction Ackermann qui est une
fonction qui croit très lentement, et qui est inférieure à 5 dans les
cas pratiques (cf. [Tar75] pour l’étude de complexité).
Lors de la création des volumes pour la construction du niveau 0, à
chaque face est associé un arbre union-find étant le seul élément de
son ensemble. Lors de la suppression d’une arête de degré deux, les deux
arbres union-find des faces incidentes à l’arête (face(d)
et face(β2(d))) sont fusionnées. Avec ce principe,
tester si β2(d) ∈ ⟨β1⟩(d) se fait simplement en
testant si find(d)=find(β2(d)). En utilisant
les heuristiques sur les arbres union-find et l’étude de la
complexité amortie des opérations, tester si une arête est de degré un
s’effectue alors en temps constant, et la complexité de la
construction de la carte de niveau 2 est linéaire en le nombre de
brins de la carte.
Lorsque l’arête est de degré un, il reste à tester si elle est
pendante ou non. La Fig. 4.22 montre les quatre
configurations possibles d’une arête de degré un en fonction du degré
des sommets de l’arête. Pour chaque sommet, nous distinguons le cas du
sommet de degré un car le sommet est alors uniquement incident à
l’arête supprimée, du cas du sommet de degré supérieur à un car le
sommet est alors incident à au moins deux arêtes. Il y a deux cas
distingués par sommet, et une arête est composée de deux sommets (car
la carte de niveau 2 ne peut pas contenir de boucle), ce qui donne les
quatre cas possibles de la Fig. 4.22. Pour
chacun de ces cas, nous sommes capables de caractériser localement la
configuration correspondante par un simple test sur le voisinage d’un
brin de l’arête, les formules étant données dans la légende de la
figure. De plus, chaque test est réalisé en temps constant. Les deux cas des
Figs. 4.4.2 et
4.4.2 sont les cas des arêtes pendantes, les
deux autres cas sont des arêtes fictives car l’arête considérée est de
degré un mais non pendante.
| Figure 4.22: Les quatre configurations possibles de faces autour d’une
arête de degré un en fonction du degré de ses sommets. (a) Les
deux sommets sont de degré un : l’arête est isolée et donc
fictive (de degré un et non pendante). β0(b)=β2(b) et
β1(b)=β2(b). (b) Une arête pendante : un sommet est
de degré un, l’autre de degré supérieur à
un. β0(b)=β2(b) et β1(b) ≠ β2(b).
(c) Une arête pendante : cas symétrique avec
β1(b)=β2(b) et β0(b) ≠ β2(b). (d) Les
deux sommets sont de degré supérieur à un, l’arête est fictive
(de degré un et non pendante). β0(b)≠ β2(b) et
β1(b)≠ β2(b). |
Nous avons prouvé que les simplifications effectuées pour calculer le
niveau 2 à partir du niveau 1 préservent la topologie de la partition
en montrant que les propriétés suivantes sont vérifiées :
-
il existe une bijection entre les surfaces du niveau 1 et les
surfaces du niveau 2;
- chaque face frontière entre deux régions de l’image est
représentée par une face homéomorphe à un disque topologique ;
- la caractéristique d’Euler de chaque surface reste constante
entre le niveau 1 et le niveau 2.
Le premier point garantit que les surfaces présentes dans la carte de
niveau 1 sont préservées dans la carte de niveau 2 ; le second point
garantit que chaque face est représentée par une seule orbite
⟨β1⟩ et donc que les surfaces sont représentées par des
complexes cellulaires 2D, et le dernier point garantit que la
topologie des surfaces est préservée (cf. [Dam08] pour plus
de détails sur les propriétés des niveaux et les preuves).
Ces trois propriétés permettent de prouver que les nombres de Betti
restent inchangés entre le niveau 1 et le niveau 2. En effet, le
nombre de composantes connexes et le nombre de cavités sont donnés par
le nombre de surfaces frontières : chaque région est représentée par
une surface frontière pour son bord externe, et une surface frontière
par cavité. Le nombre de tunnels est quant à lui lié au nombre de
surfaces frontières, et à la caractéristique d’Euler de chaque surface
(cf. Section 2.1.4 page ??).
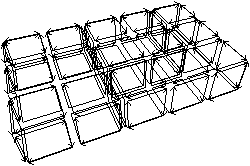
Nous pouvons voir Fig. 4.23 la carte de niveau 2 de
l’exemple utilisé Fig. 4.18. Cette carte est
désormais composée de 16 sommets, 18 arêtes, 6 faces, et 4 volumes.
[a
]
[b
]
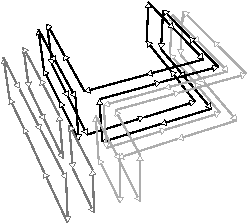
| Figure 4.23: Le niveau 2 d’une image 3D. (a) La carte de niveau 1 de
la Fig. 4.18. (b) La carte de niveau 2 dans
laquelle toutes les arêtes de degré deux et les arêtes pendantes
ont été supprimées. |
4.4.3 Le Niveau 3
La dernière passe de simplification concerne la suppression de
sommets. Comme en dimension 2, nous devons supprimer les sommets
supprimables et de degré deux afin de ne pas supprimer un sommet
incident à une seule arête (cas du sommet supprimable mais de degré
un), et pour ne pas supprimer un sommet incident à deux boucles
(cas du sommet de degré deux mais non supprimable). En effet, dans les
deux cas, la suppression du sommet entraînerait la disparition des
arêtes et des faces incidentes, et donc la disparition d’une relation
d’adjacence entre les volumes incidents. Mais un traitement spécifique
est nécessaire pour obtenir une carte ne dépendant pas de la
position des arêtes fictives. Ce traitement est basé sur le décalage
des arêtes fictives.
Nous appelons sommet
fictif un sommet incident
uniquement à des arêtes fictives, et par opposition sommet
réel un sommet incident à au
moins une arête réelle.
La Def. 70 donne la définition de la carte de niveau 3
intégrant la suppression des sommets supprimables et de degré deux et
le décalage des arêtes fictives.
Définition 70 (carte de niveau 3)
La carte de niveau 3
est la carte
obtenue à partir de la carte de niveau 2 en traitant
successivement chaque sommet s :
-
si s est un sommet réel : supprimer s s’il est est
supprimable et de degré deux après avoir décalé toutes les arêtes
fictives incidentes à s.
- si s est un sommet fictif : s’il existe une arête a non
boucle incidente à s, décaler toutes les autres arêtes
incidentes à s, puis supprimer a (ce qui supprime également
s).
Cette définition distingue deux cas pour les sommets réels et les
sommets fictifs (cf. exemples Fig. 4.24). Tout d’abord
pour les sommets réels, il existe au moins une arête réelle
incidente. Le sommet doit être supprimé s’il est supprimable et de
degré deux après avoir décalé toutes les arêtes fictives lui étant
incidentes. Les deux conditions (supprimable et de degré deux) sont
identiques au cas 2D et proviennent des mêmes considérations :
chercher à supprimer les sommets entre deux arêtes distinctes en
préservant les boucles qui sont les bords de faces frontières. Mais
avant de tester ces conditions, nous commençons par décaler toutes les
arêtes fictives incidentes au sommet. En effet, ces arêtes sont
nécessaires pour préserver la topologie de la partition en
conservant chaque face homéomorphe à un disque topologique, mais la
position de ces arêtes n’est pas importante. Afin de garantir
l’obtention de la carte minimale en nombre de cellules, nous devons
garantir qu’un sommet n’est pas non supprimable à cause de la présence
d’une arête fictive. En effet, nous obtiendrions alors une carte non
minimale puisqu’il existe une autre carte avec moins de cellules,
obtenue en changeant la position de l’arête fictive. L’étape de
décalage des arêtes fictives résout ce problème en garantissant qu’un
sommet réel est supprimé indépendamment de la position des arêtes
fictives.
[a
]
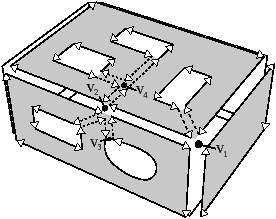
[b
]
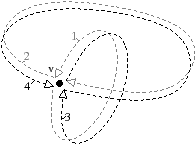
| Figure 4.24: Les différents cas possibles de sommets : fictifs ou non,
supprimables et de degré deux ou non. (a) Deux sommets satisfont
les conditions de la Def. 70 et seront
supprimés : v2 est non fictif, supprimable et de degré deux
après avoir décalé les arêtes fictives incidentes ; v4 est
fictif, supprimable et de degré deux après avoir décalé les
arêtes fictives incidentes sauf une arête non boucle. Deux
sommets ne satisfont pas les conditions et seront conservés :
v1 est de degré trois après avoir décalé les arêtes
fictives ; v3 est de degré un après avoir décalé les arêtes
fictives. (b) Cas d’une représentation minimale d’un tore : le
seul sommet v n’est pas supprimé car il est fictif et il
n’existe pas d’arête non boucle incidente à v. |
L’opération de décalage d’arête présentée au
chapitre 3 (page ??)
préserve la topologie de la partition car chaque arête décalée est ici
de degré un. De ce fait, la modification est locale à la face et la
seule modification topologique qui pourrait se produire est la
déconnexion de la face en deux, ce qui n’est pas possible. De plus, il
est facile de vérifier que le nombre de cellules de la partition reste
constant avant et après le décalage d’arête. Dans la définition du
niveau 3, après avoir décalé toutes les arêtes fictives incidentes au
sommet réel, ce sommet n’est plus incident à une arête fictive et nous
pouvons donc tester simplement s’il est supprimable et de degré deux.
Si une arête réelle incidente au sommet considéré est une boucle, le
sommet ne sera soit pas supprimable, soit pas de degré deux, ce qui
garantit qu’aucune face ne disparaisse de par la suppression du
sommet.
Pour les sommets fictifs, le principe est un peu différent : en effet,
le décalage ne peut pas concerner toutes les arêtes fictives
incidentes au sommet (car ce serait alors toutes les arêtes), mais il
concerne toutes les arêtes fictives sauf une arête non boucle. Il y a
donc deux sous cas selon qu’il existe une arête non boucle incidente
au sommet ou non. Dans le premier cas (par exemple le sommet v4
dans la Fig. 4.4.3), plusieurs arêtes fictives dont au
moins une non boucle se rejoignent «au milieu» d’une
face. Cette configuration n’est pas minimale car les arêtes fictives
servent uniquement à préserver la face homéomorphe à un disque. Il est
possible dans ce cas de décaler toutes les arêtes sauf une non boucle,
puis de supprimer cette arête qui est devenue pendante. Nous obtenons
alors une carte avec moins de cellules et représentant les mêmes
informations topologiques. Il faut noter que s’il existe plusieurs
arêtes fictives non boucle incidentes au sommet, les configurations
obtenues sont isomorphes quel que soit le choix de l’arête a
utilisée pour le décalage des autres arêtes.
Le deuxième cas est celui d’un sommet fictif pour lequel il n’existe
pas d’arête non boucle incidente. Ce cas correspond à la
configuration minimale d’un tore à k tunnels, comme le sommet v de
l’exemple de la Fig. 4.4.3. Dans cette configuration,
le sommet ne peut alors pas être supprimé sans entraîner la
suppression de la face entière incidente au sommet et donc la perte de
l’information topologique représentée par cette face frontière. Pour
cette raison ce type de sommet est conservé dans la
Def. 70.
En pratique, nous testons les propriétés des sommets avant d’effectuer
le décalagage des arêtes fictives pour des raisons d’efficacité.
Pour cela, nous parcourons chaque arête incidente au sommet courant,
en comptant le nombre d’arêtes non fictives #anf, ainsi que le
nombre d’arêtes réelles et arêtes fictives non boucles #arnb et
#afnb (ces nombres peuvent être calculés par un algorithme
linéaire en nombre de brins incidents au sommet, en marquant les
arêtes rencontrées). Si #anf>0, le sommet est réel, sinon il est
fictif. Dans les deux cas, nous pouvons facilement caractériser les
deux conditions de la Def. 70 :
-
cas d’un sommet réel : #anf>0 (sommet réel), #anf=2
(deux arêtes réelles), et #arnb=0 (les arêtes réelles ne sont
pas des boucles) ;
- cas d’un sommet fictif : #anf=0 (sommet fictif), et
#afnb>0 (il existe au moins une arête non boucle) ;
[a
]
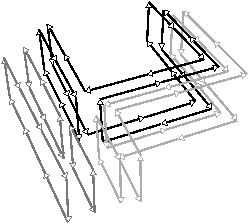
[b
]

| Figure 4.25: Le niveau 3 d’une image 3D. (a) La carte de niveau 2 de
la Fig. 4.23. (b) La carte de niveau 3 dans
laquelle tous les sommets de degré deux ont été supprimés. |
Nous pouvons voir Fig. 4.25 la carte de niveau 3 de
l’exemple utilisée Fig. 4.23. Cette carte est
désormais composée de 2 sommets, 4 arêtes, 6 faces, et 4 volumes. Elle
est minimale : il n’est pas possible de supprimer une cellule en
conservant toutes les faces frontières de l’image, et chaque face
homéomorphe à un disque. Nous pouvons prouver que le processus de
décalage d’arête couplé à la suppression de sommet permet bien
d’obtenir un minimum global quel que soit la position initiale des
arêtes fictives. En effet, les sommets sont considérés sans tenir
compte de la position des arêtes fictives. De ce fait, au moment de
traiter un sommet s, soit il satisfait les conditions de la
Def. 70 et il est supprimé, soit il ne pourra jamais
les satisfaire, quel que soient les autres suppressions et décalages
effectués ultérieurement.
4.4.4 La Carte Topologique
La carte de niveau 3 est, de manière similaire à la carte de niveau 2
en 2D, la carte combinatoire minimale représentant la partition de
l’image en régions. Mais comme en 2D, nous devons ajouter un arbre
d’imbrication des régions pour positionner entre elles les
éventuelles composantes connexes de la carte. Cet arbre repose sur le
même principe qu’en dimension 2 : les régions appartenant à la même
composante 18-connexe sont regroupées au sein d’un même ensemble, ce
qui permet de retrouver directement un brin par surface bordant les
cavités d’une région donnée (cf. les explications données en
Section 4.3.3, les seules différences étant le remplacement
de la 4-connexité 2D en 6-connexité 3D, et de la 8-connexité 2D en
18-connexité 3D).
[a
]
[b
]

[c
]
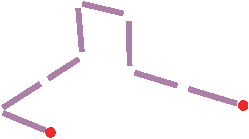
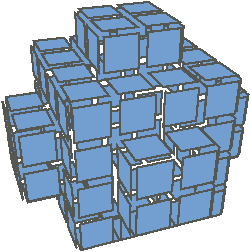
| Figure 4.26: Exemples de plongements géométriques associés à différentes
cellules de la carte. (a) Une face sphérique représentée par un
ensemble de surfels. Cette face n’a pas de bord, donc aucun lignel
n’est allumé. (b) Une face représentée par un ensemble de
surfels, et bordée par une arête (une boucle) représentée par un
ensemble de lignels. L’arête n’a pas de bord, il n’y a pas de
pointel allumé. (c) Une arête représentée par un ensemble de
lignels, ayant ses deux sommets extrémités allumés. |
Pour décrire la géométrie, nous utilisons la même solution qu’en 2D :
une matrice d’éléments intervoxels dans laquelle sont allumés les
éléments appartenant aux frontières des régions (cf. les exemples de
la Fig. 4.26) :
-
chaque surfel séparant deux voxels de régions différentes est
allumé ;
- chaque lignel incident à plus de deux surfels est allumé ;
- chaque pointel incident à un ou à plus de deux lignels est allumé.
Chaque brin de la carte est associé avec un triplet (pointel, lignel,
surfel) qui permet de retrouver la géométrie de n’importe quelle
cellule non fictive. Les cellules fictives (sommets et arêtes) n’ont
pas de géométrie car leur rôle est purement topologique. De plus, il
n’est pas toujours possible d’associer à une arête fictive une courbe
simple de lignels (par exemple dans le cas d’un tore à quatre trous,
la carte correspondante est composée de huit arêtes fictives. Il n’est
alors pas possible d’associer une géométrie à ces huit arêtes qui se
rejoignent uniquement à leur extrémités en un même pointel, étant
donné qu’un pointel peut être au maximum incident à six lignels).
La géométrie d’un sommet est directement obtenue par le pointel. La
géométrie d’une arête est l’ensemble des lignels obtenus par un
parcours dans la matrice à partir du lignel orienté du triplet
(l’orientation du lignel est donnée par le couple (pointel,lignel)), en
avançant de lignel en lignel jusqu’à tomber sur un pointel allumé ou à
revenir sur le lignel initial. La géométrie d’une face est l’ensemble
des surfels obtenus par un parcours dans la matrice à partir du surfel
orienté (l’orientation étant donnée par le triplet), en parcourant tous
les surfels voisins du surfel courant, non séparés par un lignel
(cf. exemple Fig. 4.26 et l’article
[Dam08] pour plus de détails).
Il existe un cas particulier pour les pointels incidents à un seul
lignel. Ce cas se produit lorsqu’un lignel est incident à quatre
surfels mais incident uniquement à deux régions (cf. exemple
Fig. 4.27). Dans ce cas, le
lignel est allumé car il est incident à plus de deux surfels, et les
pointels extrémités du lignel sont incidents uniquement à ce
pointel. Ces pointels doivent être allumés dans la matrice, afin que
les extrémités de chaque arête non boucle soient bien composées de deux
pointels allumés. Ce cas n’est pas possible pour les lignels, car un
lignel ne peut pas être incident à un seul surfel par définition des
régions et des frontières.
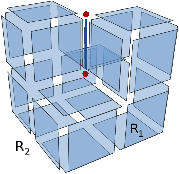
| Figure 4.27: Configuration où les deux pointels sont allumés alors
qu’ils ne sont incidents qu’à un seul lignel. La surface
représentée sépare les deux régions R1 et R2. Les pointels
représentent le plongement des sommets du bord de l’arête. |
Comme en 2D, nous appelons carte topologique
le modèle composé de la carte combinatoire de niveau 3, de l’arbre
d’imbrication des régions, et d’une représentation de la géométrie
(cf. exemple Fig. 4.28). Comme en 2D, le
choix du modèle utilisé pour représenter la géométrie dépendra des
besoins des applications, et n’est pas crucial pour nous, les
principales difficultés portent en effet sur la définition du modèle
minimal préservant les informations topologiques.
[a
]
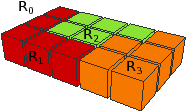
[b
]
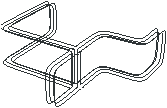
[c
]
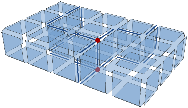
[d
]
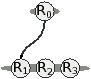
| Figure 4.28: Exemple de carte topologique 3D. (a) Une image 3D
étiquetée. (b) La carte combinatoire minimale représentant la
partition ; (c) La matrice intervoxel représentant la géométrie
des régions ; (d) L’arbre d’imbrication des régions. |
Nous pouvons voir Fig. 4.29 les différents cas
résolus par la conservation des arêtes fictives. En effet,
contrairement à la déconnexion de volume qui se produit uniquement en
présence d’imbrication, le problème de déconnexion de face se pose
lorsqu’une surface possède plusieurs bords. De plus, un problème se
pose également pour les surfaces sans bord. Dans ces cas, la solution
à base d’arbre d’imbrication n’est pas adaptée pour trois raisons :
-
la relation entre les différents bords de la face n’est pas
forcément une relation d’imbrication (cf. exemple
Fig. 4.4.4) ;
- les faces sans bord ne sont pas du tout représentées dans la
carte (cf. exemple Fig. 4.4.4) ;
- la donnée des différents bords de la face ne contient pas toutes
les informations topologiques. En effet, deux faces peuvent être
identiques pour leurs bords mais pas topologiquement équivalentes
(cf. les deux cas des Figs. 4.4.4 et
4.4.4 où les surfaces n’ont pas le même
genre).
| Figure 4.29: Le problème de représentation de faces selon leur nombre de
bords (en noir et épais sur les figures). (a) Une face comportant
3 bords, sans relation d’imbrication entre eux. (b) Une face sans
bord. (c) et (d) Deux surfaces avec les mêmes bords mais pas la
même topologie. |
La préservation des arêtes fictives résout tous ces problèmes. En
effet, avec ce type d’arête, chaque face de la carte est homéomorphe à
un disque et le genre de chaque surface peut toujours être calculé en
comptant le nombre de cellules la composant et en utilisant la formule
d’Euler-Poincaré. En effet, ce type d’arête permet :
-
de ne pas avoir de déconnexion de face, une face est représentée
dans une seule composante connexe, et ses bords sont liés
(cf. exemple Fig. 4.4.4) ;
- une surface sans bord est tout de même représentée par une ou
plusieurs arêtes fictives permettant de retrouver la topologie de la
surface (cf. exemple Fig. 4.4.4) ;
- deux surfaces topologiquement différentes ayant les mêmes bords
sont différenciées grâce à ces arêtes fictives (cf. exemple
Figs. 4.4.4 et
4.4.4).
[a
]
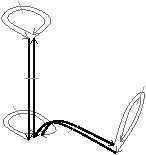
[b
]

[c
]
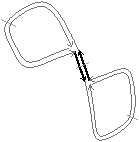
[d
]
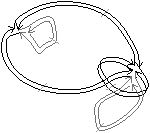
| Figure 4.30: Représentation avec des arêtes fictives des exemples de
la Fig. 4.29. Les arêtes fictives sont
dessinées en noir. La suppression de ces arêtes entraîne la
disparition de l’objet ou une déconnexion de face. |
4.5 Les Opérations
Après avoir défini le modèle des cartes topologiques, nous nous sommes
intéressés à la définition d’opérations sur ces modèles. La première
opération que nous avons étudiée est l’opération d’extraction qui
permet de construire une carte topologique à partir d’une image
étiquetée. Cette phase est en effet l’étape préalable à toutes les
autres opérations. Nous avons ensuite étudié les opérations de fusion
et de division de régions, qui sont les opérations de base permettant
de modifier la subdivision de l’image en régions. De plus, ces
opérations nous permettent par la suite de définir des algorithmes de
segmentation utilisant la carte topologique. Nous donnons ici
simplement les principes généraux de ces opérations sans rentrer dans
le détail. Le lecteur intéressé pourra trouver plus d’informations dans
les différentes références indiquées lors de la présentation des
opérations.
4.5.1 Des Algorithmes d’Extraction
Nous avons proposé
trois algorithmes permettant de construire la carte topologique, en 2D
et 3D, à partir d’une image étiquetée. Un premier algorithme, dit
naïf, consiste à construire la carte de niveau 0 puis à la
simplifier progressivement selon les définitions des différents
niveaux (cf. Fig. 4.31 pour une illustration en
2D). Cet algorithme a l’avantage d’être simple. Son inconvénient
principal est de devoir créer la carte de niveau 0 qui peut contenir
énormément de brins. De ce fait, cette carte peut ne pas tenir en
mémoire et donc empêcher le calcul de la carte minimale, malgré le
fait qu’elle contienne beaucoup moins de brins.
| Figure 4.31: Le principe de construction naïf d’une carte topologique 2D.
(a) Une image 2D étiquetée. (b) La carte de niveau 0
initiale. (c) La carte de niveau 1 obtenue après suppression
de chaque arête séparant deux pixels de même étiquette.
(d) La carte de niveau 2 obtenue après la
suppression de chaque sommet supprimable et de degré deux. |
Pour résoudre ce problème, nous avons proposé un second algorithme
d’extraction, dit par balayage. Son principe consiste à balayer
l’image (cf. la Fig. 4.32 pour une
illustration en 2D). Pour chaque pixel/voxel, un carré/cube est créé,
et ajouté à la carte en cours de construction. Pour cela, nous
conservons un brin correspondant à l’élément précédent du parcours,
qui permet de raccrocher le nouvel élément. Ensuite, la carte est
localement simplifiée autour du nouvel élément, en supprimant les
cellules caractérisées dans les définitions des niveaux de
simplification. L’avantage de cet algorithme est de ne pas
représenter toute la carte de niveau 0 en mémoire puisque les
simplifications sont effectuées de manière progressive. De plus, afin
de traiter simplement les éléments situés au bord de l’image, nous
avons créé un bord initial qui est replié sur lui-même (cf. exemple
Fig. 4.5.1). Ce bord revient à replier
l’image 2D sur un cylindre, en identifiant les pixels à droite de
l’image avec les pixels à gauche de l’image et sur la ligne suivante,
ce qui ramène le parcours de l’image à toujours avancer le pixel
courant.
[a
]

[b
]
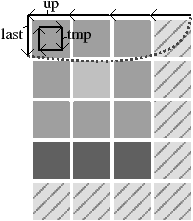
[c
]

[d
]

[e
]

…[f
]

[g
]

[h
]

| Figure 4.32: Déroulement de quelques étapes de la construction par balayage de
la carte topologique représentant une image 2D étiquetée. Les
pixels hachurés appartiennent à la région infinie. Le trait
pointillé représente la relation β1 permettant de
«fermer» le bord. (a) La carte initiale représentant le
bord supérieur et gauche (correspondante à l’image de la
Fig. 4.5.1). (b) Création et couture du carré
représentant le pixel (1,1). (c) Les cellules sont localement
simplifiées autour du pixel (1,1) lorsqu’elles vérifient les
conditions. (d) Création et couture du carré représentant le
pixel (2,1). (e) Carte obtenue après le traitement du pixel
(2,1). (f) Création du carré associé à un pixel (4,1)
appartenant à la dernière colonne. (g) Carte obtenue après le
traitement du pixel (4,1). Comme l’image est plaquée sur un
cylindre, cette configuration est équivalente à la carte présentée
en (h). |
En 3D, nous effectuons deux repliements afin de replier l’image sur un
tore volumique. De ce fait, le balayage de l’image se ramène également
à uniquement faire avancer le voxel courant (cf. [Dam01] pour
plus de détails. La version 2D est également décrite précisément dans
[DBF04] et celle 3D dans [Dam08]). Cet algorithme
a une complexité linéaire en nombre d’éléments de l’image. De plus, il
nécessite un seul balayage, le calcul de l’arbre d’imbrication des
régions étant réalisé dans une seconde étape, après l’extraction de la
carte, avec un algorithme linéaire en le nombre de brins de la carte.
Enfin, nous avons défini un troisième algorithme d’extraction, dit
optimal, utilisant la notion de
précode. Un précode est une configuration locale
de pixels/voxels dans une fenêtre de taille 2n (n étant la
dimension de l’espace, donc 2 ou 3). Le principe de cet algorithme
est d’associer à chaque précode possible un traitement modifiant
localement la carte (cf. les deux exemples de la
Fig. 4.33). L’algorithme d’extraction se ramène
alors à balayer l’image (de manière similaire à l’algorithme par
balayage) et à appliquer la modification associée au précode courant.
Cet algorithme est alors optimal car pour chaque configuration, il
effectue un nombre minimal d’opérations de mise à jour de la carte. En
2D, il existe 15 précodes différents. En découpant l’étude de ces
précodes en fonction des niveaux de simplification, nous avons montré
que des configurations pouvaient être factorisées en introduisant la
notion de précode partiel, un précode
dans lequel certain pixels/voxels peuvent avoir n’importe quelle
valeur. Cette factorisation nous a amené à réduire le nombre de cas à
10, sans aucun surcoût de traitement. Le gain n’est pas très important
en 2D mais il devient beaucoup plus intéressant en dimension 3 où le
nombre total de précodes existant est de 4140, ce qui rend difficile
le développement de toutes les fonctions associées. En factorisant ces
précodes à l’aide de la notion de précode partiel, nous avons réduit
le nombre de cas à 379, et l’avons encore diminué à 129 en regroupant
les configurations symétriques. Ce nombre de cas reste important, mais
le développement des différentes fonctions redevient envisageable, ce
qui n’était pas le cas avec le nombre initial de cas. Une première
version de cet algorithme à base de précodes a été présentée dans
[BDF00]. La version 2D est décrite dans
[DBF04], et la version 3D est décrite en détail dans
[Dam01].
| Précode | Carte initiale | Carte finale |
 | 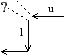 | 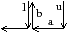 |
 | 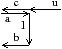 | 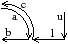 |
| Figure 4.33: Deux exemples de précodes, le premier étant un précode
partiel. Pour chaque précode, il faut transformer la carte
initiale en la carte finale. Cette transformation est équivalente
à la création d’un carré représentant le pixel, puis à la
suppression locale des cellules autour de ce pixel. Mais
l’opération est ici optimale car nous évitons la création inutile
de brins, et nous réutilisons lorsque c’est possible les brins
existants. |
4.5.2 Fusion / Découpe de Régions
Les premières opérations de modification que nous avons définies sont la
fusion et la découpe de régions. Ce travail a été initié durant le
stage de master recherche de Patrick Resch [DR02, DR03]
avant d’être poursuivi et généralisé durant la thèse d’Alexandre Dupas
[DD08a, DD09, Dup09]. Les opérations présentées ici le
sont pour les cartes topologiques 3D, mais sont bien entendu définies
pour les cartes topologiques 2D de manière équivalente.
De manière générale, l’opération de fusion va s’appuyer sur les
opérations de suppression, et l’opération de découpe va s’appuyer sur
les opérations d’insertion. La principale difficulté des opérations de
modification dans le cadre des cartes topologiques est de garantir la
préservation des propriétés de ce modèle, c’est-à-dire principalement
la minimalité de la carte combinatoire, et conserver chaque face
homéomorphe à un disque. Il faut également garantir le lien cohérent
entre la carte combinatoire et l’arbre d’imbrication des régions, la
propriété sur le brin représentant, et le lien entre la carte et le
plongement géométrique. Pour simplifier les modifications, nous
découpons souvent l’opération en deux étapes : la première étape
effectue les modifications sans se préoccuper des contraintes, et la
deuxième étape s’occupe uniquement des mises à jour liées à ces
contraintes.
La première opération définie est la fusion de régions. Nous avons
proposé deux approches pour cette opération (détaillées dans les
Algorithmes 4.34 et 4.5.2) : la
première, dite fusion locale, qui va fusionner un ensemble
connexe de régions dans une seule région ; la seconde approche, dite
fusion globale, qui va effectuer la fusion simultanée de
plusieurs ensembles de régions connexes, chaque ensemble étant
fusionné dans une région. Nous avons comparé ces approches et montré
que la première est plus intéressante dans le cadre d’un faible nombre
de régions à fusionner, comme par exemple dans une utilisation
interactive où les régions sont sélectionnées par un utilisateur, et
que la seconde est plus intéressante dans le cadre de la fusion d’un
grand nombre de régions, comme par exemple dans le cas d’une
segmentation d’images par agrégation de régions.
| Figure 4.34: Algorithme : Approche locale de la fusion de régions |
-
Entrées : Une carte topologique C;
Un ensemble 6-connexe de régions E.
- Résultat : Fusionne les régions de E dans C.
choisir la plus petite région de E comme région résultante;
Pour chaque brin b appartenant aux régions de E faire
Si region(β3(b)) ∈ E alors
marquer b et β3(b);
mettre à jour l’arbre d’imbrication des régions;
supprimer toutes les faces intérieures (préalablement marquées);
simplifier les cellules incidentes aux faces supprimées;
L’Algorithme 4.34 donne le principe général de l’approche
locale de la fusion. Il comporte trois étapes principales :
-
calcul de la région résultante et marquage des faces intérieures
(c-à-d les faces entre deux régions à fusionner);
- mise à jour de l’arbre des régions pour prendre en compte les
modifications possibles de l’arbre d’imbrication;
- mise à jour de la carte combinatoire et du plongement dans la
matrice intervoxel en supprimant les faces intérieures et en
simplifiant si besoin les arêtes et sommets incidents.
La première étape garantit que le brin représentant b de la région
résultante de l’union vérifiera bien la contrainte des brins
représentants (c-à-d par β3, nous obtenons un brin d’une
région plus petite que la région de b). Ensuite, le marquage des
faces intérieures se fait simplement en testant pour chaque brin b
des régions de S si β3(b) est un brin d’une région de E. Si
oui la face est intérieure aux régions de l’ensemble et elle devra
être supprimée. La mise à jour de l’arbre d’imbrication va consister à
supprimer les régions de E et à les remplacer par une seule région,
mais également à détecter des éventuelles nouvelles imbrications
créées par la fusion. Cette étape est réalisée avant la suppression
des faces intérieures afin de pouvoir utiliser ces faces pour
retrouver les futures relations d’imbrication. Ensuite, il reste à
mettre à jour la carte combinatoire, tout d’abord en supprimant les
faces intérieures (en utilisant les opérations de 2-suppression, tout
en mettant également à jour la géométrie dans la matrice
d’inter-éléments), puis en simplifiant la carte pour la rendre
minimale (en utilisant les définitions des différents niveaux, et les
opérations de 1- et 0-suppression).
L’approche globale de la fusion de régions consiste à fusionner
simultanément plusieurs ensembles 6-connexes de régions. Son
principe est de séparer les modifications de la carte topologique du
processus de fusion de régions proprement dit. Dans un premier temps,
les régions sont manipulées avec un haut niveau d’abstraction, à
l’aide d’arbres union-find. Puis, dans un second temps, les
fusions de haut niveau sont retranscrites dans la partition
représentée par une carte topologique en supprimant les cellules
inutiles et en construisant le nouvel arbre d’imbrication des régions.
L’Algorithme 4.5.2 présente le principe de la fusion de
régions par approche globale. Il prend en paramètres une carte
topologique C et une fonction Oracle qui indique si deux régions
doivent être fusionnées. L’algorithme modifie la carte topologique de
sorte que tous les ensembles 6-connexes de régions désignés par
l’oracle soient effectivement fusionnés dans la partition finale. Il
comporte trois étapes principales :
-
fusion des régions à haut niveau d’abstraction : c’est la fusion
symbolique ;
- mise à jour de la carte combinatoire minimale et de la matrice
intervoxel ;
- construction du nouvel arbre d’imbrication.
| Figure 4.35: Algorithme : Approche globale de la fusion de régions |
-
Entrées : Une carte topologique C ;
Une fonction Oracle. - Résultat : Fusionne toutes les régions par composante 6-connexe en
fonction de l’oracle.
Pour chaque brin b ∈ C faire
Si Oracle(region(b),region(β3(b))) alors
fusionner symboliquement region(b) et region(β3(b));
supprimer toutes les faces intérieures;
simplifier la carte topologique;
construire le nouvel arbre d’imbrication des régions;
Lors de la première étape de l’algorithme, chaque région est
initialisée comme racine de son propre arbre union-find. La
fusion symbolique de deux régions consiste alors simplement à faire
l’union des deux arbres union-find correspondants. À la fin de
cette étape, chaque arbre union-find est un ensemble
6-connexe de régions à fusionner. Un brin b appartient à une face
intérieure si region(b)=region(β3(b)). Les étapes suivantes de
l’algorithme sont identiques à celles de la fusion locale : supprimer
les faces intérieures, simplifier la carte et mettre à jour l’arbre
d’imbrication. La différence avec la fusion locale est que ces
modifications sont faites sur toute la carte, et non plus de manière
locale. De ce fait, nous préférons reconstruire totalement l’arbre
d’imbrication plutôt que de le mettre à jour : en effet, comme le
nombre de modifications dans cet arbre peut être important, il est
moins coûteux de le recalculer entièrement.
L’opération inverse de la fusion de régions est la division d’une
région. L’objectif est d’obtenir plusieurs régions en découpant une
région initiale. De manière générale, la division de région utilise
un guide, par exemple une surface, pour découper la région
initiale. Le nombre de régions résultantes dépend alors de la
géométrie de la région initiale et de la géométrie du guide utilisé
pour la découpe. Une division particulière est l’éclatement d’une
région. Il s’agit de la division d’une région de manière à ce que
chaque région résultante ne contienne qu’un seul voxel.
L’Algorithme 4.5.2 présente les différentes opérations
réalisées pour éclater une région en régions élémentaires. Il prend
comme paramètres une carte topologique et une région à éclater.
| Figure 4.36: Algorithme : Éclatement d’une région en régions élémentaires |
-
Entrées : Une carte topologique C;
Une région R. - Résultat : Éclatement dans C de la région R en régions élémentaires.
D ← ensemble de brins vide;
Pour chaque surface S du bord de R faire
ajouter l’un des brins de S à D;
éclater le volume incident aux brins de D en volumes
élémentaires;
construire une nouvelle région par volume;
mettre à jour l’arbre d’imbrication;
simplifier les bords des régions éclatées;
Son principe consiste à éclater chaque surface bordant la région R
en ce que nous appelons des volumes élémentaires. Un volume
élémentaire est un volume qui correspond à un voxel de l’image (de
même pour une face/arête élémentaire pour les surfels/lignels). Cette
étape se réalise en insérant des sommets sur les bords des faces
jusqu’à avoir des arêtes élémentaires. Puis nous saturons chaque face
en insérant toutes les arêtes possibles jusqu’à obtenir uniquement des
faces élémentaires, et enfin nous saturons le volume en insérant
toutes les faces possibles jusqu’à obtenir uniquement des volumes
élémentaires (cf. exemple Fig. 4.37). Nous associons
ensuite une nouvelle région à chaque volume élémentaire et mettons à
jour l’arbre d’imbrication des régions en remplaçant la région éclatée
par ces nouvelles régions, et en modifiant éventuellement les
relations d’imbrication qui existaient avec R. Enfin, nous devons
simplifier le bord des nouvelles régions car il se peut que celles
touchant le bord de R aient des cellules non minimales.
[a
]
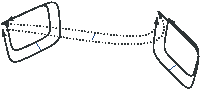
[b
]
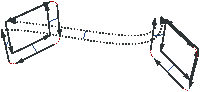
[c
]
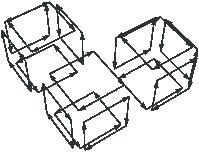
[d
]
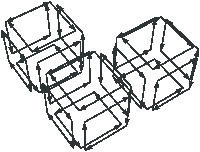
| Figure 4.37: Exemple d’éclatement d’une région en volumes
élémentaires. (a) La région initiale composée de trois faces :
deux représentées par une seule arête qui est une boucle, et une
troisième qui est composée de trois arêtes, dont une
fictive. (b) Résultat après l’éclatement des arêtes non fictives
en arêtes élémentaires. (c) Résultat après la saturation des
faces : chaque face de la région est maintenant
élémentaire. (d) Carte finale obtenue après la saturation de la
région en volumes élémentaires. |
L’éclatement d’une région construit une partition généralement
sursegmentée de la région initiale. Une partition aussi détaillée
n’est pas souhaitable dans la plupart des applications. D’une part le
temps de calcul de cette opération est long, et d’autre part l’espace
mémoire nécessaire pour représenter la partition éclatée est très
important, surtout lorsque la région éclatée est grande. Nous avons
donc défini une opération de division d’une région qui est plus
adaptée aux besoins pratiques : la division de régions par un guide.
Le guide est donné par un ensemble de surfels qui doit être séparant,
c’est-à-dire couper la région R en au moins deux régions.
L’Algorithme 4.5.2 présente l’opération de division d’une
région par un guide. Il prend en paramètres une carte topologique, une
région et un ensemble de surfels qui est un guide de division pour la
région sélectionnée.
| Figure 4.38: Algorithme : Division d’une région par un guide |
-
Entrées : Une carte topologique C ;
Une région R ;
Un guide G. - Résultat : Division dans C de la région R par le guide G.
éclater les arêtes et les faces du bord de la région R;
construire le guide de division défini par G;
coudre le guide aux bords de la région R;
construire l’arbre d’imbrication des nouvelles régions;
simplifier la carte topologique;
La première étape de l’algorithme consiste à éclater le bord de la
région à diviser en faces élémentaires, de manière similaire à l’étape
d’éclatement d’une région, mais sans effectuer la dernière étape qui
éclate les volumes. L’étape suivante construit le guide de division
dans la carte topologique, en construisant une face carrée par surfel
du guide, et en cousant correctement ces faces entre elles selon les
configurations des surfels dans G. Ce guide est ensuite fusionné
dans la carte topologique. Comme nous avons éclaté le bord de la
région R, et par construction du guide, nous n’avons que des arêtes
élémentaires. La fusion consiste alors simplement à interclasser les
faces autour des arêtes du bord du guide. Le résultat de cette
opération est le remplacement du volume associé à la région R par
l’ensemble des volumes décrits par le guide et les bords de la région
(cf. exemple Fig. 4.39). Il faut alors effectuer la
mise à jour de l’arbre d’imbrication, puis simplifier la carte pour
la rendre minimale.
[a
]

[b
]
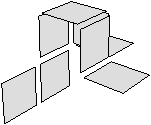
[c
]
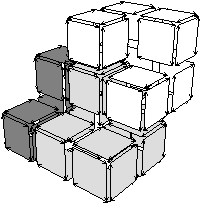
| Figure 4.39: Exemple de découpe d’une région par un guide. (a) La
région initiale après que son bord ait été éclaté en faces
élémentaires. (b) Le guide utilisé pour découper cette
région. (c) Résultat obtenu après l’insertion du guide dans la
région qui est découpée en trois volumes. Il reste à simplifier
les bords de ces volumes et à mettre à jour l’arbre
d’imbrication. |
4.6 Conclusion
Dans ce chapitre, nous avons défini la carte topologique 2D et 3D, un
modèle de représentation d’une image étiquetée. Ce modèle utilise une
carte combinatoire minimale afin de représenter la partition de
l’image en cellules ainsi que les relations d’incidence et
d’adjacence entre ces cellules. Cette carte est liée à un modèle
décrivant la géométrie de ses cellules, qui peut être une matrice
d’inter-éléments, mais qui peut aisément être changé selon les besoins
des applications. Enfin, un arbre d’imbrication des régions permet de
compléter la représentation du modèle en décrivant les relations entre
les différentes composantes connexes de la carte.
La carte topologique est définie de manière progressive, en utilisant
les opérations de base définies au
chapitre 3. Cette définition progressive simplifie
les définitions ainsi que l’étude des problèmes de déconnexion, car
chaque niveau est défini par l’application d’un seul type
d’opération. C’est ce type de définition qui nous a permis d’étendre
de manière assez directe la carte topologique 2D en dimension
supérieure, chose qui semblait beaucoup plus délicate avec les modèles
proposés précédemment dans la littérature, soit de par leur définition
directe, soit à cause de leur algorithme de construction. Cette
définition progressive a également simplifié la définition
d’algorithmes d’extraction à partir d’une image, en facilitant
l’intégration progressive des opérations de simplification, et en
proposant un moyen direct de regrouper les cas à traiter.
Nous avons également présenté brièvement quelques opérations définies
dans le cadre des cartes topologiques : tout d’abord l’extraction
d’une carte topologique à partir d’une image étiquetée, puis les
opérations de fusion et de découpe qui sont les opérations de
modification de base d’une carte topologique.
Nous avons dans ce chapitre utilisé les cartes combinatoires, mais
comme l’ensemble des définitions utilisent les opérations de base, ces
définitions sont également valides sans aucune modification pour les
cartes généralisées. Le choix des cartes combinatoires a été ici guidé
par le développement d’un logiciel (présenté
chapitre 7) qui demande deux fois moins d’espace
mémoire pour les cartes combinatoires que pour les cartes
généralisées.
Nous souhaitons poursuivre ces travaux afin d’étendre la carte
topologique en dimension quelconque. Les niveaux de simplification
s’étendent de manière directe : en dimension n, une carte
topologique serait définie par n niveaux de simplification, chaque
niveau i, 1≤ i ≤ n étant la simplification du niveau i−1
en utilisant la (n−i)-suppression. Un arbre d’imbrication serait
utilisé pour conserver les relations entre les différentes
composantes connexes de la carte. Le seul problème qui reste
partiellement ouvert est celui des éléments fictifs. Pour tout i,
1≤ i < n−1, nous aurions des i-cellules fictives pour
conserver chaque (i+1)-cellule homéomorphe à une boule. La
conservation de ces cellules doit pouvoir se faire en détectant les
cellules de degré un, mais cela doit être étudié plus précisément. Par
contre, pour obtenir la carte minimale, nous devons décaler ces
cellules afin qu’elles n’empêchent pas d’autres suppressions. C’est ce
point qui reste à étudier plus précisément : le décalage de
i-cellule, et son utilisation pour garantir la préservation de la
topologie des objets, tout en garantissant également l’obtention de la
carte minimale. Nous allons également poursuivre le développement
d’autres opérations, pour proposer un ensemble d’outils permettant
de réaliser la plupart des opérations possibles de traitement
d’images.
Nous allons maintenant présenter une extension hiérarchique des cartes
que sont les pyramides généralisées. L’objectif de ce modèle est de
manipuler différentes représentations d’un même objet, par exemple afin
de conserver plusieurs niveaux de détails, ou pour décrire différentes
subdivisions d’un même objet, chacune pouvant correspondre à une
sémantique particulière. Ces pyramides sont à nouveau définies à partir
des opérations de base présentées au chapitre précédent.



 [b]
[b]




 [b
[b [c
[c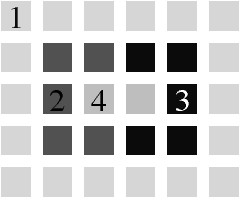




 [b
[b
 [b
[b
 [b
[b
 [b
[b
 [b
[b
 [b
[b
 [b
[b
 [b
[b [c
[c


 [b
[b
 [b
[b
 [b
[b
 [b
[b
 [b
[b
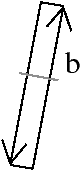 [b
[b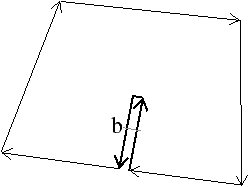 [c
[c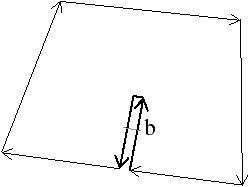 [d
[d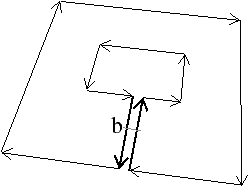
 [b
[b
 [b
[b
 [b
[b
 [b
[b [c
[c

 [b
[b [c
[c [d
[d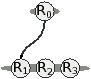
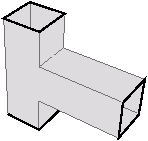 [b
[b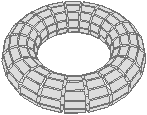 [c
[c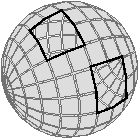 [d
[d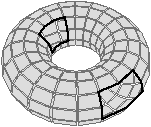
 [b
[b [c
[c [d
[d
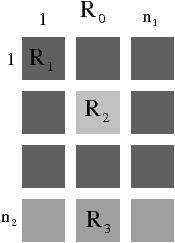 [b
[b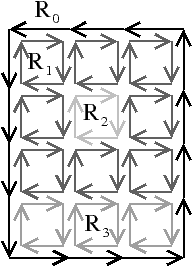 [c
[c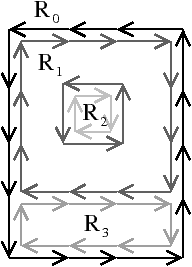 [d
[d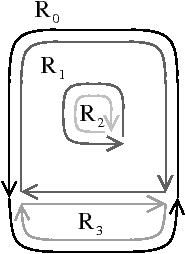
 [b
[b [c
[c [d
[d
 …[f
…[f [g
[g [h
[h

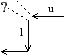
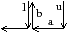


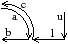
 [b
[b [c
[c [d
[d
 [b
[b [c
[c