 [b]
[b]
| Figure 6.1: Exemple de schéma polygonal. (a) Un polygone composé de quatre arêtes, et la subdivision du tore correspondante. (b) Un polygone composé de six arêtes, et la subdivision du tore correspondante. |



Après avoir défini les modèles combinatoires de représentation de subdivisions dans les chapitres précédents, nous nous intéressons maintenant aux opérations de calcul d’invariants topologiques. En effet, un des intérêts des modèles présentés est qu’ils décrivent la topologie des objets manipulés. Il est donc important d’être capable d’utiliser ces informations au sein d’opérations, et pour cela il est nécessaire de pouvoir calculer des invariants topologiques.
Une spécificité de notre approche est l’utilisation des opérations de suppression et contraction pour simplifier un objet donné, ce qui permet soit de calculer plus simplement l’invariant topologique recherché, soit d’accélérer ce calcul car le nombre de cellules est beaucoup moins important. Pour cela, nous devons garantir que les opérations de simplification ne modifient pas la topologie de l’objet ce qui assure l’absence de perte d’information par rapport à l’objet initial. Nous faisons dans ce chapitre cette étude pour l’opération de suppression, le cas de la contraction pouvant se déduire directement par propriété de dualité. En dimension n, nous étudions seulement la caractéristique d’Euler-Poincaré. Nous avons également étudié trois autres invariants : les nombres de Betti, le schéma polygonal canonique, et les groupes d’homologie, mais pour le moment uniquement en 2D ou 3D.
Nous avons introduit Section 2.1.4 (page ??) la notion d’invariant topologique, et détaillé deux invariants numériques : la caractéristique d’Euler-Poincaré et les nombres de Betti. Nous allons montrer dans ce chapitre comment calculer ces invariants sur des objets décrits par des cartes. Mais avant, nous commençons par introduire Section 6.1 deux autres invariants topologiques qui sont le schéma polygonal canonique (un polygone canonique décrivant une surface) et les groupes d’homologie (des invariants classiques de la topologie algébrique).
Nous présentons simplement les notions de base des groupes d’homologie, et seulement de manière intuitive, le lecteur intéressé pourra consulter les références [Gib81, Hat02]. Ensuite, nous présentons Section 6.2 la mise à jour locale des nombres de cellules d’une subdivision lors des opérations de simplification, ce qui fournit directement un algorithme de calcul de la caractéristique d’Euler-Poincaré. Puis, Section 6.3, nous utilisons ce résultat pour proposer un algorithme de calcul des nombres de Betti d’une subdivision 3D orientable. Section 6.4 nous donnons une méthode de calcul du schéma polygonal canonique d’une surface 2D fermée, et Section 6.5 nous présentons deux algorithmes de calcul des groupes d’homologie 2D, et 3D dans le cas où l’objet est orientable. La Section 6.6 conclut et donne des perspectives à ce chapitre.
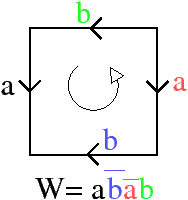
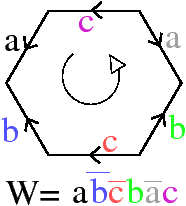
Toute surface S (2-variété) fermée peut être représentée par un polygone P, appelé schéma polygonal [Sti80, Gib81]. C’est un polygone dans lequel chaque arête est orientée et étiquetée avec une lettre de telle manière que chaque lettre soit l’étiquette de deux arêtes différentes du polygone. Ce polygone correspond à la surface obtenue en identifiant chaque couple d’arêtes ayant la même étiquette, en respectant l’orientation (cf. exemple Fig. 6.1).
Pour obtenir un schéma polygonal à partir d’une surface, il faut tout d’abord subdiviser la surface en sommets, arêtes et faces, orienter chaque arête de manière arbitraire, et étiqueter chaque arête avec une lettre distincte des lettres utilisées pour les autres arêtes. Il faut alors découper au maximum la surface le long des arêtes de la subdivision, jusqu’à ce que la surface soit homéomorphe à un disque. Il ne reste plus qu’à supprimer les arêtes se trouvant au milieu de la surface afin d’obtenir un seul polygone, qui lorsque les arêtes de même étiquette sont identifiées en respectant l’orientation, va donner une surface homéomorphe à la surface initiale.
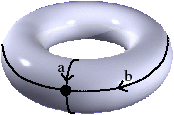
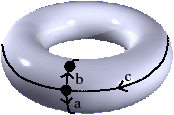
Il existe plusieurs schémas polygonaux associés à la même surface, ce qui complexifie la comparaison des surfaces. L’exemple de la Fig. 6.1 montre deux schémas polygonaux qui sont tous deux associés à un tore. Il est possible d’associer un mot à chaque schéma polygonal en partant d’une arête du polygone et en lisant les lettres rencontrées en tournant dans un sens donné, sachant qu’une lettre est inversée lorsque l’arête est d’orientation opposée par rapport au sens de parcours. Pour l’exemple de la Fig. 6.1, en partant de l’arête a à gauche sur le dessin, et en tournant dans le sens trigonométrique, nous obtenons le mot abab, et pour l’exemple de la Fig. 6.1, le mot obtenu à partir de l’arête étiquetée a à gauche sur le dessin est le mot abcbac. Ce mot est cyclique car l’arête de départ du polygone est quelconque : par exemple les mots abcbac et acabcb sont identiques.
[a]
[b]


Figure 6.1: Exemple de schéma polygonal. (a) Un polygone composé de quatre arêtes, et la subdivision du tore correspondante. (b) Un polygone composé de six arêtes, et la subdivision du tore correspondante.
Pour résoudre ce problème de différents schémas polygonaux représentant la même surface, le schéma polygonal canonique a été défini [Bra22, VY90, FK97]. Ce schéma polygonal est unique et caractérise la topologie de la surface. Il est en lien direct avec le théorème de classification des surfaces (cf. Théorème 1 Section 2.1.4, page ??). Il existe trois formes différentes selon le type de surface considérée :
Tous les sommets du polygone associé au schéma polygonal canonique sont identifiés en un seul sommet, et toutes les arêtes sont donc des boucles (sauf dans le cas de la sphère).
Par exemple, le schéma polygonal canonique d’un tore est le mot abab (c’est l’exemple de la Fig. 6.1), le schéma polygonal canonique du plan projectif est le mot aa, et celui de la bouteille Klein (qui est la somme connexe de deux plans projectifs) est aabb.
Grâce au théorème de classification des surfaces, nous savons que le schéma polygonal canonique classifie totalement la topologie de la surface qu’il représente. Mais ce type de théorème n’existant pas en 3D, nous devons utiliser des invariants topologiques afin de décider si deux surfaces sont topologiquement différentes. Un invariant particulièrement intéressant pour cela est l’homologie. Le principe est d’associer à tout espace topologique X de dimension n une famille de n+1 groupes commutatifs, appelés groupes d’homologie. Ces groupes sont caractérisés par des générateurs qui sont en bijection avec des sous-ensembles de cellules de la subdivision, chaque générateur étant défini à homotopie près (les éléments de chaque classe pouvant s’obtenir par des déplacements continus). De ce fait, les groupes d’homologie peuvent être décrits de manière algébrique par ces ensembles de cellules.
Une i-chaîne (chaîne de dimension i) est une somme formelle de i-cellules. Dit autrement, c’est un ensemble pondéré de i-cellules, la pondération étant signée. À partir de ces i-chaînes est défini le groupe des chaînes Ci. L’opérateur de bord ∂ est défini pour chaque i-cellule c, i ∈ {1,…,n}, et donne une somme pondérée sur l’ensemble des (i−1)-cellules du bord de c. Le bord d’une i-chaîne est alors simplement la somme du bord de ses i-cellules (c’est une (i−1)-chaîne). Un cycle est une chaîne dont le bord est nul. Un bord est une i-chaîne qui est l’image d’une (i+1)-chaîne par l’opérateur de bord. L’ensemble des cycles (resp. bords) de dimension i de X est noté Zi(X) (resp. Bi(X)). La propriété principale de l’opérateur de bord est que pour toute chaîne c, c ∂ ∂ =0, c-à-d le bord d’une chaîne est nécessairement un cycle, qui donc n’a lui-même pas de bord. Deux chaînes c1 et c2 sont homologues si elles diffèrent par un bord. Dans ce cas, une chaîne peut s’écrire comme la somme de l’autre chaîne et d’un bord. La notion de chaîne homologue est une relation d’équivalence, et les groupes d’homologie sont définis par le quotient du groupe des cycles par cette relation d’équivalence. De ce fait, tout élément de Hi(X) est un cycle qui n’est pas un bord. Dit autrement, ∀ i ∈ {0,…,n}, le ième groupe d’homologie est noté Hi(X). Il est obtenu en quotientant le groupe des cycles par le sous-groupe des bords : Hi(X)=Zi(X)/Bi(X).
Les nombres de cellules d’une subdivision n’est pas un invariant topologique, mais sert au calcul des invariants topologiques numériques que sont la caractéristique d’Euler-Poincaré et les nombres de Betti.
Pour calculer ces nombres de cellules dans une carte (généralisée ou combinatoire), il suffit d’utiliser la définition de cellule, et pour chaque dimension de l’espace, de compter le nombre d’orbites distinctes. Cela donne un algorithme en O(n · k), où n la dimension de l’espace et k le nombre de brins de la carte. Mais lorsque ces nombres sont utilisés dans un algorithme itératif qui modifie la subdivision (comme dans l’application de segmentation avec contrôle topologique présentée Section 7.2), faire ce calcul à chaque étape de l’itération s’avère trop coûteux.
Pour régler ce problème, nous avons proposé un algorithme de mise à jour de ces nombres de cellules lors des opérations de suppression. Le principe de cet algorithme consiste à calculer une première fois les nombres de cellules (par exemple en utilisant la méthode comptant le nombre d’orbites) puis à les mettre à jour lors des opérations de suppression.
Lorsqu’une i-cellule est supprimée, cela modifie bien évidemment le nombre de i-cellules qui diminue de un, mais selon les configurations, d’autres modifications peuvent se produire :
Ces modifications possibles, qui ne sont pas exclusives, nous amènent à la Prop. 9 de mise à jour des nombres de cellules pour l’opération de suppression.
Il y a deux cas différents : le premier pour l’évolution du nombre de i-cellules qui diminue toujours de un, et le second pour tenir compte des trois types de modifications évoquées ci-dessus : fusions, disparitions, ou déconnexions de j-cellules, avec j ≠ i. La prise en compte correcte de ces trois cas nécessite de compter le nombre de j-cellules incidentes à c avant et après la suppression de c, le nombre de j-cellules étant alors simplement mis à jour en effectuant la différence entre ces deux nombres.
De ce fait, dans ces trois cas, la mise à jour du nombre de cellules va être correctement réalisée. (1) Si c séparait deux (i+1)-cellules distinctes qui sont fusionnées après la suppression, nous allons avoir e1=2 et e2=1, le nombre de (i+1)-cellules diminue de un (cf. l’exemple de la Fig. 6.2). (2) Si une j-cellule est incluse dans c, cette cellule va être comptée dans les cellules avant la suppression mais pas après et donc le nombre de j-cellules va bien diminuer de un (cf. l’exemple de la Fig. 6.4). (3) Si une j-cellule est déconnectée en trois j-cellules après la suppression, le nombre de j-cellules va augmenter de deux (cf. l’exemple de la Fig. 6.6).
Compter les nombres de cellules avant et après la suppression revient à compter des nombres d’orbites. Pour le nombre de j-cellules incidentes à c avant la suppression, nous avons directement e1=|{⟨h(αj)⟩(b)|b∈ c}|. Pour le nombre de j-cellules incidentes à c après la suppression, nous devons considérer les brins j-voisins de c qui n’appartiennent pas à c : vc=c αj∖ c. Ce sont les brins survivants «autour» de c. Le nombre de j-cellules incidentes à c après la suppression est alors e2=|{⟨h(αj)⟩(b)|b∈ vc}| en considérant la carte obtenue après l’opération de suppression.
Nous illustrons ces modifications dans différentes configurations. Tout d’abord, la Fig. 6.2 présente le cas général de la 2-suppression, lorsque la face supprimée est de degré deux, et qu’il n’existe pas d’arête uniquement incidente à cette face. La suppression de la face entraîne que le nombre de volumes diminue de un (deux volumes différents sont fusionnés), et que le nombre de faces diminue de un également (la face supprimée). La caractéristique d’Euler-Poincaré (qui est la somme alternée du nombre de cellules) est donc inchangée.
[a][b]
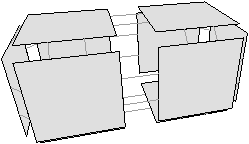
Figure 6.2: Cas général de 2-suppression d’une face de degré deux, sans arête uniquement incidente à cette face. (a) Carte initiale. La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face. Le nombre de volumes diminue de un (deux volumes différents sont fusionnés), et le nombre de faces diminue de un également : la caractéristique d’Euler-Poincaré est inchangée.
Dans la Fig. 6.3, la face supprimée f est de degré un et aucune de ses arêtes n’est incidente seulement à f. Le nombre de faces diminue de un et les autres nombres de cellules restent constants, ce qui entraîne la diminution de un de la caractéristique d’Euler-Poincaré. Il faut noter ici que la carte obtenue ne vérifie plus les conditions de la Def. 45 de caractéristique d’Euler cellulaire (page ??). De ce fait, cette caractéristique n’est plus valide, même si les nombres de cellules sont correct.
[a][b]
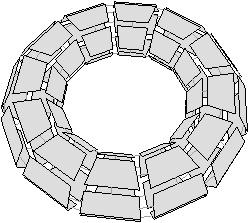
Figure 6.3: 2-suppression d’une face de degré un, sans arête uniquement incidente à cette face. (a) Carte initiale. La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face. Le nombre de faces diminue de un, les autres nombres de cellules restent constants : la caractéristique d’Euler-Poincaré diminue de un.
Dans l’exemple de la Fig. 6.4, la face supprimée f est de degré un, et trois de ses arêtes sont incidentes uniquement à f. Le nombre de faces diminue de un, le nombre d’arêtes diminue de trois, et le nombre de sommets diminue de deux. La caractéristique d’Euler-Poincaré est donc ici inchangée.
[a][b]
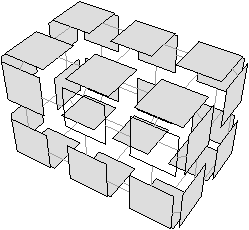
Figure 6.4: 2-suppression d’une face de degré un, ayant trois arêtes incidentes uniquement à la face supprimée. (a) Carte initiale (deux faces sont dessinées en fil-de-fer pour visualiser l’intérieur du volume). La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face, qui a entraîné la disparition des trois arêtes et des deux sommets incidents uniquement à cette face. Le nombre de faces diminue de un, le nombre d’arêtes de trois, et le nombre de sommets de deux : la caractéristique d’Euler-Poincaré est inchangée.
Dans l’exemple de la Fig. 6.5, la face supprimée f est de degré un, et deux de ses arêtes (non adjacentes1) sont incidentes uniquement à f. Le nombre de faces diminue de un, et le nombre d’arêtes diminue de deux : la caractéristique d’Euler-Poincaré augmente de un.
[a][b]
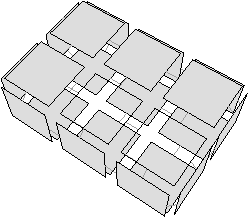
Figure 6.5: 2-suppression d’une face de degré un, ayant deux arêtes non adjacentes incidentes uniquement à la face supprimée. (a) Carte initiale (deux faces sont dessinées en fil-de-fer pour visualiser l’intérieur du volume). La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face, qui a entraîné la disparition des deux arêtes incidentes uniquement à cette face. Le nombre de faces diminue de un, et le nombre d’arêtes diminue de deux : la caractéristique d’Euler-Poincaré augmente de un.
Dans l’exemple de la Fig. 6.6, la carte initiale est composée d’un seul volume, car la face à supprimer f est reliée à elle-même par α2 le long de l’arête supérieure. Après la suppression de f, ce volume se trouve déconnecté en trois volumes distincts. Cela entraîne une diminution de un du nombre de faces et une augmentation de deux du nombre de volumes. Le nombre d’arêtes diminue également de un car une arête est incluse dans f.
[a][b]
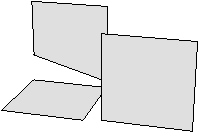
Figure 6.6: 2-suppression d’une face entraînant la déconnexion d’un volume en plusieurs volumes. (a) Carte initiale. La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face, qui a entraîné la déconnexion du volume en trois volumes. Le nombre de faces diminue de un, le nombre de volumes augmente de deux, et le nombre d’arête diminue de un.
Dans l’exemple de la Fig. 6.7, un volume incident à la face supprimée f est inclus dans f. La suppression de f entraîne la disparition de ce volume et donc le nombre de 3-cellules diminue de un. Comme le nombre de faces diminue également de un, la caractéristique d’Euler-Poincaré est inchangée.
[a][b]
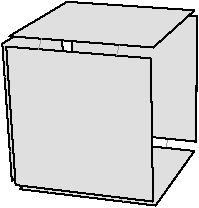
Figure 6.7: 2-suppression d’une face entraînant la disparition d’un volume. (a) Carte initiale. La face à supprimer est en gris foncé. (b) Carte obtenue après la suppression de la face, qui a entraîné la disparition du volume qui était incident uniquement à cette face. Le nombre de faces diminue de un, et le nombre de volumes diminue de un : la caractéristique d’Euler-Poincaré est inchangée.
Les deux exemples des Figs. 6.8 et 6.9 montrent l’évolution du nombre de cellules lors de la suppression d’arête. Dans le premier cas, le nombre de faces diminue de un (deux faces sont fusionnées), le nombre d’arêtes diminue de un et le nombre de sommets n’est pas modifié car les deux sommets de l’arête a ne sont pas incidents uniquement à a. La caractéristique d’Euler-Poincaré reste donc constante.
[a][b]
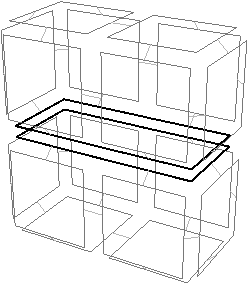
Figure 6.8: 1-suppression de l’arête incidente au brin b qui est de degré deux. (a) Carte initiale. (b) Carte obtenue après la suppression de l’arête qui a entraîné la fusion des deux faces en une. Le nombre de faces diminue de un, et le nombre d’arêtes aussi : la caractéristique d’Euler-Poincaré est inchangée.
Dans le second exemple de la Fig. 6.9, l’arête est pendante, donc un sommet est incident uniquement à l’arête. Le nombre de faces reste alors constant, le nombre d’arêtes diminue de un, et le nombre de sommets diminue également de un, ce qui fait que la caractéristique d’Euler-Poincaré reste également inchangée.
[a][b]
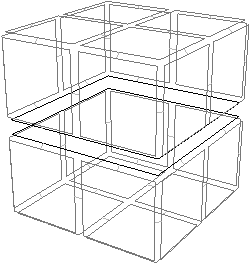
Figure 6.9: 1-suppression de l’arête incidente au brin b qui est pendante. (a) Carte initiale. (b) Carte obtenue après la suppression de l’arête qui a entraîné la disparition du sommet incident uniquement à cette arête. Le nombre d’arêtes diminue de un, et le nombre de sommets aussi : la caractéristique d’Euler-Poincaré est inchangée.
Cette mise à jour nécessite donc le parcours des j-cellules incidentes à c, afin de compter leur nombres avant et après la suppression. Même si dans le pire des cas toutes les cellules de la carte sont incidentes à c, il est clair que dans la majorité des cas le nombre de cellules à tester sera petit en comparaison du nombre de brins de la carte car cela reste un traitement local.
Ces modifications des nombres de cellules de la subdivision nous donnent directement un algorithme permettant de calculer la caractéristique d’Euler-Poincaré lors des opérations de suppression, sous réserve que la carte vérifie les conditions de la caractéristique d’Euler cellulaire. De plus, en utilisant la dualité suppression/contraction, la Prop. 9 s’étend directement aux opérations de contraction :
Enfin, il est possible d’utiliser ce principe de mise à jour du nombre de cellules pour stocker et mettre à jour le nombre de cellules de chaque région d’une carte.
Une région R est un élément de dimension n, ayant un bord externe (une quasi variété de dimension n−1) et k bords internes entourant les cavités de R (k quasi-variétés). Une région sans cavité (k=0) est équivalente à une n-cellule, mais ce n’est pas vrai pour les régions avec cavités (cf. le chapitre 4 où nous avons utilisé cette notion de région dans le cadre cartes topologiques).
Nous associons alors à chaque région son nombre initial de cellules, puis mettons à jour ces nombres lors des opérations de suppression (cela nous servira Section 6.3 pour le calcul des nombres de Betti des régions).
Cela entraîne deux types de changements par rapport à ce que nous venons de présenter, où les cellules étaient comptées de manière globale à toute la carte, alors qu’elles sont maintenant comptées indépendamment pour chaque région :
Pour la (n−1)-suppression d’une cellule c, il y a deux cas différents selon si c est incidente à deux régions distinctes ou à une seule région (cf. Prop. 11).
Dans le premier cas, nous devons calculer le nombre de cellules de la nouvelle région qui est la fusion des deux régions initiales. Pour cela, nous commençons par additionner les nombres de cellules de R1 et de R2. Mais certaines cellules peuvent alors être comptées deux fois : ce sont les cellules qui étaient incidentes aux deux régions R1 et R2. Pour chacune de ces i-cellules, le nombre de i-cellules de la région résultante est diminuée de un ce qui fait que la cellule est désormais bien comptée une seule fois. Il ne reste plus qu’à utiliser la propriété précédente de mise à jour des nombres de cellules pour l’opération de suppression (donnée Prop. 9) sur la région résultante pour tenir compte des modifications entraînées par la (n−1)-suppression de c. Dans le cas où la cellule supprimée est incidente à une seule région R, la modification est plus simple puisqu’il suffit alors d’utiliser directement la Prop. 9 car il n’y a alors pas de fusion de régions.
Pour les autres opérations, que ce soit la i-suppression, avec 0≤ i<n−1, ou la i-contraction, avec 1≤ i≤ n, les Props. 9 et 10 sont toujours valides, mais elles doivent êtres appliquées pour chaque région incidente à la cellule concernée. Par exemple la suppression d’une arête en 3D va modifier le nombre de cellules de toutes les régions autour de cette arête. Cette modification se fait simplement en parcourant l’orbite de la cellule supprimée ou contractée, et en appliquant la définition correspondante pour chaque nouvelle région rencontrée.
Nous avons utilisé ces propriétés de mise à jour des nombres de cellules de chaque région lors des opérations de suppression dans [DPFL06] pour compter ces nombres durant l’extraction de la carte topologique 3D. Comme cette extraction s’effectue par un balayage de l’image voxel par voxel, nous avons pu éviter le premier calcul global des nombres de cellules en initialisant ces nombres lors de la création de nouvelles régions. En effet, une région est toujours initialement associée à un seul voxel et nous pouvons donc fixer ses nombres de volumes, faces, arêtes et sommets à un, six, douze et huit. Nous utilisons ensuite les formules données ci-dessus pour mettre à jour ces nombres de cellules lors des opérations de suppression. Nous avons pu simplifier, et donc optimiser, la mise à jour des nombres de cellules en utilisant les propriétés spécifiques liées aux propriétés de la carte topologique et de l’algorithme d’extraction. À la fin de l’extraction de la carte topologique, nous avons directement les nombres de cellules de chaque région, avec un surcoût presque nul par rapport à l’algorithme initial (cf. [DPFL06] pour plus de détails). Ces nombres nous servent ensuite à calculer la caractéristique d’Euler-Poincaré, soit de la subdivision globale, soit de chaque région. Nous avons également utilisé ces nombres comme outils de base pour calculer les nombres de Betti.
De manière similaire au calcul de la caractéristique d’Euler-Poincaré, nous avons proposé deux méthodes permettant de calculer les nombres de Betti d’une région dans une carte (combinatoire ou généralisée) : une méthode directe, et une seconde méthode utilisant les opérations de suppression et la mise à jour locale des nombres de cellules. Ce travail est pour le moment limité aux objets 3D orientables, et une perspective est son extension à tout type de quasi-variété. Par contre, il est valide pour les cartes combinatoires et les cartes généralisées car il se base sur les nombres de cellules qui sont définis pour les deux modèles. Ce travail est un résultat de la thèse d’Alexandre Dupas [Dup09] et a été présenté dans [DD09].
Pour calculer les nombres de Betti d’une région R donnée, nous utilisons les propriétés présentées à la section précédente permettant de calculer le nombre de cellules de chaque région d’une carte. Nous notons χ′(R) la somme alternée (le nombre sommets moins le nombre d’arêtes plus le nombre de faces) des cellules de la région R. Ce nombre n’est pas la caractéristique d’Euler-Poincaré de la région R dans le cas où elle possède des cavités ou des tunnels (car la région n’est alors pas homéomorphe à une boule, donc la carte n’est pas un complexe cellulaire). Mais nous allons voir dans ce chapitre que ce nombre peut être utilisé pour calculer la caractéristique d’Euler-Poincaré et donc les nombres de Betti.
La première méthode permettant de calculer les nombres de Betti consiste à utiliser directement χ′(R), et le nombre de surfaces bordant la région R. Comme nous ne considérons ici que des objets 3D orientables plongés dans ℝ3, seuls les trois premiers nombres de Betti sont significatifs (b0, b1 et b2), les autres étant tous nuls.
b0(R) est toujours égal à un car il compte le nombre de composantes connexes de l’objet, et nous calculons le nombre de Betti d’une région qui est connexe par définition (un objet non connexe à nécessairement plusieurs bords externes).
Nous étudions maintenant b2, car nous verrons par la suite que b1 se déduit des autres nombres. b2(R) compte le nombre de cavités de la région R. Ce nombre est égal au nombre de surfaces bordant R, noté #s(R), moins un. En effet, le bord de chaque région est composé d’une surface externe, et de k surfaces internes, une par cavité de la région. Pour calculer #s(R), nous devons retrouver toutes les surfaces bordant la région R. Cette information n’est pas contenue dans la carte, et il est nécessaire d’avoir une structure de données supplémentaire la représentant. Nous avons présenté au chapitre 4 l’arbre d’imbrication des régions qui est une réponse à ce besoin, et que nous réutilisons ici. L’avantage de cet arbre est que les régions imbriquées sont regroupées par composantes connexes. De ce fait, chaque région R a pour fils direct un représentant par composante connexe, et donc le nombre de surfaces internes de la région est exactement le nombre de ses fils directs, noté fils(R).
Il reste à étudier b1(R) qui compte le nombre de tunnels de la région R. Ce nombre est lié à la caractéristique d’Euler-Poincaré par la formule χ(R)=b0(R)−b1(R)+b2(R) (cf. Def. 14). Notre démarche consiste ici à calculer χ(R). Comme nous venons de donner les formules permettant de calculer b0(R) et b2(R), cela nous permettra directement de calculer b1(R).
Nous avons vu au chapitre précédent comment calculer χ′(R), mais ce nombre peut être différent de la caractéristique d’Euler-Poincaré. Ce cas se pose lorsque la carte n’est pas un complexe cellulaire (au sens présenté au chapitre 2), c’est-à-dire si toutes ses cellules ne sont pas homéomorphes à des boules. Nous nous plaçons ici dans un cadre similaire à celui utilisé pour la carte topologique dans lequel chaque 0-cellule, 1-cellule et 2-cellule est homéomorphe à une boule, et seuls les volumes ne sont pas nécessairement des boules. Cette supposition est raisonnable pour deux raisons. Premièrement elle est toujours vraie pour les 0-cellules et les 1-cellules. Deuxièmement, le cas d’une 2-cellule non homéomorphe à une boule pose des difficultés dans la manipulation des faces. Ces problèmes sont résolus en conservant des arêtes fictives lors des opérations de suppression, ce qui préserve alors chaque face homéomorphe à une 2-boule (cf. chapitre 4).
Notre solution afin de traiter correctement le cas des régions non homéomorphes à des boules consiste à rajouter des cellules pour rendre ces régions homéomorphes à des boules, et pour lesquelles nous avons alors χ′(R)=χ(R). En pratique, ces éléments ne sont pas ajoutés dans la carte mais simplement comptés comme s’ils étaient présents : c’est la notion de cellules implicites.
La Fig. 6.10 présente deux exemples de cellules implicites. La région de la Fig. 6.3.1 contient un tunnel qui est bouché par la face implicite dessinée en gris : l’objet devient homéomorphe à une 3-boule. Dans la Fig. 6.3.1, la région contient une cavité, qui est reliée à la surface externe par une face implicite (en gris sur la figure), ce qui rend le volume de la région homéomorphe à une 3-boule. Cette face est composée de 4 arêtes, les deux arêtes noires qui existaient déjà sur les deux surfaces à relier, et les deux autres en gris qui sont des nouvelles arêtes implicites.
[a][b]
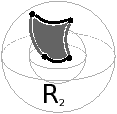
Figure 6.10: Exemples de cellules implicites (dessinées en gris foncé) pour des régions qui ne sont pas homéomorphes à des 3-boules. (a) Une région torique R1. La face implicite permet de couper le tunnel en deux et ainsi rend la région homéomorphe à une 3-boule. (b) Une région sphérique R2 ayant une cavité sphérique. L’ajout de la face implicite permet de connecter la cavité avec l’extérieur et ainsi rend la région homéomorphe à une 3-boule.
Nous pouvons maintenant utiliser ces cellules implicites pour lier χ(R) et χ′(R). En effet, χ′(R) est la somme alternée du nombre de cellules des surfaces bordant R : χ′(R)=#c0(R)−#c1(R)+#c2(R). La caractéristique d’Euler-Poincaré χ(R) est quant à elle la somme alternée du nombre de cellules du complexe cellulaire χ(R)=k0(R)−k1(R)+k2(R)−k3(R), en notant ki(R) le nombre de i-cellules du complexe cellulaire associé à la région R, en tenant compte des cellules implicites.
Il suffit d’utiliser la Def. 83 donnant les cellules implicites qui sont ajoutées pour faire le lien entre les ki(R) et les #ci(R). k0(R)=#c0(R) car il n’y a pas de sommet implicite. k1(R)=#c1(R)+2 b2(R) car il y a deux arêtes implicites ajoutées pour chaque cavité de R, et ce nombre de cavités est b2(R). Enfin, k2(R)=#c2(R)+b1(R)+b2(R) car il y a une face ajoutée pour chaque tunnel et une face ajoutée pour chaque cavité. k3(R)=1 car chaque région est connexe, donc composée d’un seul volume par définition.
En remplaçant les ki(R) par ces nouvelles écritures, nous obtenons χ(R)=(#c0(R)−#c1(R)+#c2(R))−(1−b1(R)+b2(R)). Comme χ(R)=1−b1(R)+b2(R) (cf. la Def. 14 page ?? liant les nombres de Betti et la caractéristique d’Euler-Poincaré), nous avons directement χ(R)=χ′(R)/2.
En re-écrivant la formule χ(R)=b0(R)−b1(R)+b2(R) pour calculer b1(R), nous obtenons b1(R) = b0(R) + b2(R) − χ′(R) / 2. Nous avons montré à la section précédente comment calculer χ′(R), et nous venons de voir comment calculer b0(R) et b2(R), nous pouvons donc à l’aide de cette formule calculer b1(R).
Pour résumer, les nombres de Betti d’une région R sont donnés par la proposition suivante :
Pour utiliser les nombres de Betti au sein d’algorithmes modifiant une carte à l’aide des opérations de suppression, nous avons défini une méthode de mise à jour locale de ces nombres de Betti.
Comme b0(R) est égal à 1 pour toute région R, il n’y a pas de mise à jour à réaliser.
Pour calculer b1(R), nous venons de donner une formule basée sur b0(R), b2(R) et χ′(R). Nous avons vu au chapitre précédent comment mettre à jour localement χ′(R), et b0(R) est constant. En donnant la manière de mettre à jour localement b2(R), nous serons donc directement capables de mettre à jour b1(R).
Étudions donc maintenant la mise à jour de b2(R) qui est le nombre de cavités de la région R. La mise à jour locale consiste donc à étudier les évolutions du nombre de cavités de R durant les opérations de suppression. Nous pouvons faire une première remarque qui est que le nombre de cavités est constant lors des 0-suppressions et des 1-suppressions d’une cellule non isolée et n’entraînant pas de déconnexion de cellule. En effet, ce type de suppression ne peut pas entraîner de création ou de suppression de cavités. Nous nous intéressons donc uniquement à l’opération de 2-suppression. Nous avons vu au chapitre précédent que le nombre de cavité est égal au nombre de surfaces bordant R (noté #s(R)) moins un (pour ne pas compter la surface externe). Nous étudions donc comment calculer #s(R), ce qui nous donnera directement b2(R).
Nous étudions pour cela l’impact de la suppression d’une 2-cellule c sur le nombre de surfaces bordant la région R. Nous pouvons remarquer que seules les surfaces incidentes à c sont concernées par la suppression. Comme pour les 0- et 1-suppressions, nous ajoutons une contrainte sur la 2-cellule à supprimer qui ne doit pas être isolée2. Dans ce cas, la suppression de la cellule peut soit ne pas modifier le nombre de surfaces, soit l’augmenter, mais en aucun cas le diminuer. En effet, une 2-suppression de cellule non isolée peut éventuellement déconnecter une surface en plusieurs parties (et donc augmenter le nombre de surfaces) mais ne peut pas fusionner plusieurs surfaces en une seule.
Comme pour la mise à jour locale du nombre de cellules, nous distinguons deux cas selon le type de la 2-cellule supprimée. Si c sépare deux régions distinctes R1 et R2, il y a deux surfaces incidentes à c avant la suppression (une du côté de R1 et une autre du coté de R2), et ces deux surfaces sont fusionnées en une seule après la suppression. De ce fait, le nombre de surfaces de la nouvelle région #s(R1∪ R2)=#s(R1)+#s(R2)−1 (comme ∀ R, #s(R)>0, #s(R1∪ R2)>#s(R1) et #s(R1∪ R2)>#s(R2)).
Si c est incidente à une seule région R, la mise à jour est plus complexe car nous devons tester quelles surfaces incidentes à c sont déconnectées, en étudiant le nombre de composantes connexes de l’orbite ⟨α0,α1,α2⟩ autour de c, avant et après la suppression (de manière similaire à la mise à jour locale du nombre de cellules présenté à la section précédente).
Nous proposons pour cela un algorithme qui calcule le nombre de surfaces incidentes à c qui seront disjointes après la suppression de c. Cet algorithme permet de calculer les nombres de Betti de l’union de deux régions avant de réaliser cette union, ce qui est utile dans les algorithmes souhaitant contrôler l’évolution des caractéristiques topologiques (cf. l’application de segmentation avec contrôle topologique présentée au chapitre 7).
Nous utilisons pour cela l’Algorithme 6.3.2 qui parcourt une surface, sans passer par des faces marquées .
Figure 6.11: Algorithme : Parcours de la surface en sautant les face marquées
- Entrées : Une carte combinatoire C ;
Un brin b non marqué minner ;
Une marque minner marquant les faces à ignorer.- Résultat : Parcours de la surface incidente à b en ignorant les faces marquées.
P ← pile de brins vide;
empiler b dans P;
Tant que P n’est pas vide faire
b′ ← tête de P;
dépiler P;
Si b′ n’est pas déjà traité alors
// le brin b′ appartient à la surface incidente à b
// traiter le brin
empiler β1(b′) dans P;
b2 ← β2(b′);
Tant que b2 est marqué par minner faire
b2 ← β32(b2);
empiler b2 dans P;
Le principe de cet algorithme est similaire à un parcours classique de surface. Il utilise une pile des brins à traiter, et pour un brin non traité va ajouter dans la pile les voisins de ce brin par β1 et β2. Le changement par rapport à un parcours classique de surface consiste à ne pas empiler directement le brin β2(b′) mais à sauter les éventuelles faces marquées en utilisant β32 autant de fois que nécessaire jusqu’à obtenir un brin non marqué par minner. Cela revient à simuler l’opération de 2-suppression qui redéfinit β2 de cette manière. De ce fait, la surface parcourue par cet algorithme est identique à la surface qui serait parcourue après la suppression des faces marquées minner. Cet algorithme est donné pour un ensemble quelconque de faces marquées, de manière similaire à la définition de l’opération de suppression d’un ensemble de cellules. De plus, nous l’avons donné ici pour les cartes combinatoires mais il peut être porté très simplement pour les cartes généralisées, la seule différence étant qu’il faudra parcourir α0, α1 et α2 pour parcourir la surface, et utiliser α32 pour sauter les faces marquées.
Cet algorithme de parcours de surface en sautant les faces marquées est la base de l’Algorithme 6.3.2 qui va calculer le nombre de surfaces incidentes à une 2-cellule c qui seront disjointes après la suppression de c.
Figure 6.12: Algorithme : Compte les surfaces autour d’une face après sa suppression.
- Entrées : Une carte combinatoire C ;
Un brin b.- Résultat : Le nombre de surfaces incidentes à c2(b) après la suppression de c2(b).
k ← 0;
minner, mtraite ← marques sur les brins;
marquer tout les brins de c2(b) avec minner;
Pour chaque brin d ∈ c2(b) faire
Si β2(d) n’est pas marqué par mtraite ni par minner alors
marquer avec mtraite la surface incidente à β2(d) en sautant les brins marqués par minner;
k ← k+1;
Retourner k;
Le principe de cet algorithme consiste tout d’abord à marquer avec la marque minner tous les brins de la cellule c2(b) qui va être supprimée. Ensuite, pour chaque brin de cette cellule, nous testons si le brin β2(d) n’est pas un brin déjà traité ni un brin de c2(b). En effet, dans le premier cas, sa surface a déjà été comptée, et dans le deuxième cas c’est qu’il n’y a pas de surface incidente à ce brin. Lorsque ces deux conditions sont vérifiées, la surface incidente à ce brin est marquée avec mtraite, en sautant les brins marqués minner (ce qui garantit que la surface traitée ne passe pas par la cellule c2(b)). Nous avons trouvé une nouvelle surface, et incrémentons donc le résultat de un, puis passons à un autre brin. À la fin de cet algorithme, nous avons parcouru toutes les surfaces incidentes à c2(b), et nous avons donc compté toutes les futures surfaces distinctes que nous allons obtenir après la suppression de c2(b).
Cet algorithme a une complexité linéaire en nombre de brins des surfaces incidentes à c2(b). C’est une complexité importante pour une mise à jour, mais elle reste locale en nombre de brins des cellules incidentes à la cellule supprimée.
Le nombre de surfaces de R après la suppression de c2(b) se calcule maintenant très simplement : #s(R)=#s(R)−1+k, où k est le nombre de surfaces autour de c2(b) (le résultat de l’Algorithme 6.3.2). Nous enlevons un pour enlever la surface initiale qui était incidente à c2(b), car cette surface sera comptée dans l’algorithme. Comme c2(b) n’est pas isolée, k>0 et donc nécéssairement #s(R) est inchangé ou augmente.
Nous pouvons maintenant résumer la mise à jour locale du nombre de surfaces pour la 2-suppression de la cellule c2(b) :
Cela nous donne directement la mise à jour locale de b2(R) puisqu’il est égal à #s(R)−1.
Après les nombres de Betti, nous nous intéressés à un autre invariant topologique : le schéma polygonal canonique. Après avoir étudié cet invariant, nous avons remarqué que nous obtenons le même type de résultats que ceux présentés chapitre 4 pour la carte topologique 3D, dans le cas des régions représentées par une surface fermée. Cela nous a amenés à étudier le lien entre les opérations que nous utilisons lors de la construction de cette carte topologique (les opérations de suppression et le décalage d’arête) et les opérations utilisées pour la construction du schéma polygonal canonique : ces opérations sont basées sur la découpe et le collage de la surface, et la transcription de ces opérations en terme de transformations de mots. Nous avons ainsi pu transcrire l’algorithme original [VY90] qui transforme un schéma polygonal en schéma polygonal canonique dans un algorithme effectuant la transformation similaire pour une 2G-carte [DA08].
Le premier algorithme permettant de construire un schéma polygonal canonique provient de [VY90]. Dans cet article, les auteurs définissent 5 règles de transformation, ils prouvent que ces règles préservent la topologie de la surface, et que l’application itérative de ces règles permet toujours d’obtenir le schéma polygonal canonique.
L’algorithme se décompose en deux étapes. La première consiste à transformer le schéma polygonal initial en un schéma polygonal réduit, c’est-à-dire un polygone de la forme aa dans le cas de la sphère, ou un polygone dont la subdivision de la surface associée est composée d’un seul sommet. Cette première étape est réalisée à l’aide des deux transformations A et B suivantes :
[a][b]
[c]
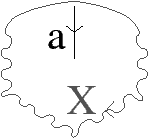
Figure 6.13: Transformation A : aaX ⇒ X. (a) Le schéma polygonal initial. (b) Les deux arêtes a sont identifiées. (c) L’arête a est effacée, car elle est à l’intérieur du polygone.
(où X et Y sont des mots quelconques, éventuellement vides).
La transformation B est découpée en deux cas selon que l’arête a est orientable3 ou non. Ces trois cas sont illustrés dans les Figs. 6.13, 6.14 et 6.15.
[a][b]
[c]
[d]
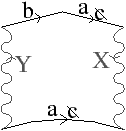
Figure 6.14: Transformation B dans le cas orientable : aXabY ⇒ baXaY. (a) Le schéma polygonal initial. (b) Le polygone est coupé pour isoler les arêtes a et b. (c) Le morceau coupé est re-collé le long de l’arête a. (d) L’arête a est effacée, car elle est à l’intérieur du polygone, et l’arête c est renommée a.
[a][b]
[c]
[d]
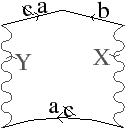
Figure 6.15: Transformation B dans le cas non-orientable : aXabY ⇒ abXaY. Les étapes sont les mêmes que dans le cas orientable, mais le résultat change de par le fait que l’arête a est non-orientable.
En utilisant ces transformations de manière itérative, un algorithme linéaire permet de transformer n’importe quel schéma polygonal en schéma polygonal réduit [VY90].
La deuxième étape de la transformation consiste à transformer ce schéma réduit en schéma polygonal canonique. Pour cela, les trois transformations C, D et E sont utilisées :
(où X et Y sont à nouveau des mots quelconques, éventuellement vides). Ces trois transformations peuvent, comme les deux précédentes, être réalisées sur le schéma polygonal par des opérations de découpe et de collage (cf. [VY90]).
Nous nous intéressons maintenant à la manière de construire le schéma polygonal d’une 2G-carte fermée, où chaque arête est représentée par quatre brins. La première étape consiste à étiqueter chaque brin de la G-carte. Pour chaque brin b n’ayant pas encore d’étiquette, nous l’étiquetons avec une nouvelle étiquette e, étiquetons le brin α2(b) avec e, et enfin nous étiquetons les deux brins α0(b) et α02(b) avec l’étiquette inverse e. L’arête incidente au brin b est donc associée à l’étiquette e, et les deux orientations possibles de l’arête ont bien des étiquettes inverses (cf. exemple de la Fig. 6.4.2).
[a][b]
[c]
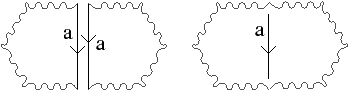
Figure 6.16: (a) Une 2G-carte ayant ses brins étiquetés : deux brins en relation par α0 ont deux étiquettes inverses, et deux brins en relation par α2 ont même étiquette. (b) 2G-carte où l’arête a a été supprimée. Le mot associé est W=dbcdcb. (c) L’opération correspondante pour obtenir un schéma polygonal consiste à coller les deux polygones le long des arêtes a et à supprimer l’arête a.
Pour construire le schéma polygonal, cette carte doit être simplifiée afin de ne contenir qu’une seule face qui est le polygone. Pour cela, chaque arête de degré 2 de la carte est supprimée. Comme nous pouvons voir Fig. 6.16, cette opération est équivalente à coller deux polygones le long d’une arête de même étiquette puis à effacer cette arête. Comme chaque arête de degré deux est supprimée, et comme la 2G-carte initiale est fermée, à la fin de cette étape la G-carte est composée d’une seule face car toutes les arêtes restantes sont de degré un (donc incidentes deux fois à la même face).
Le mot associé à cette 2G-carte et représentant le schéma polygonal est calculé en partant d’un brin b quelconque de cette carte. L’étiquette de b donne la première lettre du mot. Ensuite, la carte est parcourue en déplaçant b sur le brin α01(b), et en ajoutant la lettre obtenue à la fin du mot. Le mot est terminé lorsque b est revenu sur le brin initial (cf. Fig. 6.4.2).
Nous avons maintenant une 2G-carte composée d’une seule face, mais ayant plusieurs arêtes et sommets. La première étape de l’algorithme initial consiste à transformer ce polygone en un polygone réduit, c-à-d un polygone équivalent mais n’ayant plus qu’un seul sommet.
Nous utilisons pour cela les deux transformations A et B de l’algorithme original, en les transposant aux 2G-cartes. Pour la transformation A, le mot est de la forme aaX. Dans ce cas, l’arête a est pendante et la transformation revient à supprimer cette arête pendante (cf. Fig. 6.17).
[a][b]
[c]
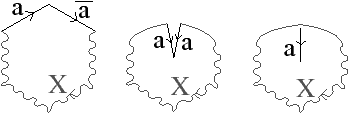
Figure 6.17: Transformation A. (a) Une 2G-carte avec une arête pendante a. (b) La 2G-carte obtenue après la suppression de l’arête a. (c) L’opération correspondante sur le schéma polygonal.
La transformation B correspond à l’opération de décalage d’arête. Nous avons exactement le même résultat que sur le polygone : l’opération utilisée est identique dans le cas orientable et le cas non-orientable, mais elle produit deux résultats différents.
Pour la transformation B dans le cas ou l’arête a est orientable (c-à-d prise deux fois dans des sens opposés), le mot associé est aXabY (avec éventuellement X ou/et Y vide). Après le décalage de l’arête a, le mot devient baXaY : la lettre qui était après a a été mise avant a (cf. Fig. 6.18).
(a) (c) (e) 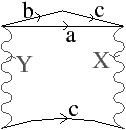
(b) (d) (f)
Figure 6.18: Transformation B dans le cas orientable. (a) Une 2G-carte avec une arête orientable a. (b) Le schéma polygonal correspondant. (c) et (d) première étape : une nouvelle arête est insérée, c, qui va couper le polygone en isolant les arêtes a et b. (e) et (f) deuxième étape : l’arête a est supprimée, en deux temps dans le schéma polygonal, puis l’arête c est renommée a.
Pour la transformation B dans le cas ou l’arête a est non-orientable (c-à-d prise deux fois dans le même sens), le mot associé est aXabY (avec éventuellement X ou/et Y vide). Après le décalage de l’arête a, le mot devient abXaY : la lettre qui était après le second a est inversée et mise après le premier a (cf. Fig. 6.19).
(a) (c) (e) 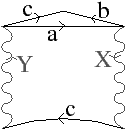
(b) (d) (f)
Figure 6.19: Transformation B dans le cas non-orientable. (a) Une 2G-carte avec une arête non-orientable a. (b),(c), (d), (e) et (f) sont les mêmes étapes que pour le cas orientable.
Pour transformer le schéma polygonal réduit en schéma polygonal canonique, les trois opérations C, D et E sont utilisées.
La transformation C transforme le mot aXaY en aaY−1X, avec a une arête non-orientable. Cette transformation peut être réalisée en décalant |Y| fois l’arête a. En effet, le mot initial peut s’écrire sous la forme aXay1… yk (les yi étant les lettres du mot Y). Nous venons de voir (pour la transformation B2) que lors du décalage d’une arête non-orientable, la lettre qui était après le second a est inversée et mise après le premier a. De ce fait, décaler l’arête a une fois va nous donner le mot ay1Xay2… yk. Le second décalage va donner le mot ay2y1Xay3… yk et ainsi de suite jusqu’à obtenir le mot aayk…y1X qui correspond bien à aY−1Xa. Le problème de cette transformation est que l’algorithme associé a une complexité en O(k), avec k le nombre de lettres du polygone.
Nous avons donc proposé un algorithme optimisé (cf. l’Algorithme 6.4.4 et Fig. 6.21) qui va effectuer la transformation C sur la 2G-carte en O(1).
1-coudre(α01(a),α201(a));
1-coudre(α1(a),α0(a));
1-coudre(a,α20(a));
Figure 6.20: Algorithme : Transformation C(a)
(a) (b)
Figure 6.21: Transformation C. (a) Une 2G-carte correspondant au mot aXaY. (b) La 2G-carte obtenue comme résultat de l’Algorithme 6.4.4 : elle correspond bien au mot aaY−1X.
Nous pouvons vérifier sur la Fig. 6.21 que l’algorithme correspond bien à la transformation C. Cet algorithme a une complexité en temps constant car il est composé d’opérations atomiques de liaison de brins qui s’effectuent en temps constant, et ce quel que soit la longueur du mot Y, ce qui n’est a priori pas évident étant donné qu’il faut inverser l’ordre et la valeur des lettres de ce mot. Mais ces transformations se font directement grâce au fait qu’une 2G-carte contient les deux orientations possibles de chaque chemin et donc de chaque mot. De ce fait, changer simplement le point d’entrée dans le mot Y revient à inverser l’ordre et la valeur des lettres (cf. Fig. 6.22).
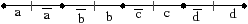
Figure 6.22: Exemple d’inversion d’un mot représenté dans une G-carte. Si le premier brin rencontré est celui étiqueté a, le mot est Y=abcd. En commençant le parcours par le dernier brin de ce chemin, étiqueté d, le mot est dcba, qui est bien égal à Y−1.
La transformation D peut, comme la C, s’effectuer de manière non optimisée en décalant plusieurs fois l’arête a et l’arête b. Mais nous pouvons également définir un algorithme optimisé, donné Algorithme 6.23 et illustré Fig. 6.24, qui effectue la modification en temps constant.
1-coudre(α1(a),α21(a));
1-coudre(α1(b),α21(b));
1-coudre(a,α201(a));
1-coudre(α01(b),α201(b));
1-coudre(α2(b),α01(a));
1-coudre(α2(a),α02(b));
1-coudre(b,α0(a));
1-coudre(α20(a),α0(b));
Figure 6.23: Algorithme : Transformation D(a,b)
(a) (b)
Figure 6.24: Transformation D. (a) Une 2G-carte correspondant au mot aXbYaUbV. (b) La 2G-carte obtenue comme résultat de Algorithme 6.23 : elle correspond bien au mot ababXVUY.
Enfin, de manière similaire, nous proposons un algorithme optimisé pour la transformation E (Algorithme 6.25 et Fig. 6.26) qui est à nouveau en O(1).
1-coudre(α0(a),α2(a));
1-coudre(α02(a),b);
1-coudre(α0(b),α2(b));
1-coudre(α02(b),c);
Figure 6.25: Algorithme : Transformation E(a,b,c)
(a) (b)
Figure 6.26: Transformation E. (a) Une 2G-carte correspondant au mot ababccX. (b) La 2G-carte obtenue comme résultat de Algorithme 6.25 : elle correspond bien au mot aabbccX.
Nous avons donc désormais tous les outils nécessaires pour calculer le schéma polygonal canonique de n’importe quelle 2G-carte fermée. Ces outils sont les briques de base utilisées dans l’algorithme original, ce qui nous donne directement notre algorithme sur les 2G-cartes. L’avantage de notre approche par rapport à la méthode initiale est que nous travaillons directement sur la subdivision et pas sur un mot associé (bien qu’il soit directement possible de retrouver ce mot). Cela évite une étape préalable de transformation de la surface, et cela permet surtout de faire le lien plus directement entre les transformations utilisées et les modifications de la surface sous-jacente. Nous souhaitons par exemple étudier comment mettre à jour la géométrie de la surface afin de pouvoir dessiner le polygone canonique sur la surface initiale, et cela sera plus simple avec notre approche qui modifie directement la subdivision qu’avec la méthode originale qui travaille sur le mot correspondant. Un autre avantage de notre approche est la transformation C que nous pouvons réaliser en O(1) et ce sans aucune structure de données annexe, chose qui n’est pas possible dans l’algorithme initial. Un autre point de recherche qu’il serait intéressant d’étudier est l’extension en 3D de la notion de schéma polygonal. En effet, la notion de schéma polyédrique a été introduite par Poincaré dans les années 1895 [Sti80], mais apparemment il y a eu très peu de travaux autour de cette notion. Avec les cartes, nous avons les outils nécessaires pour représenter et manipuler les subdivisions 3D, et cela pourrait servir de pont vers la meilleure compréhension et vers l’extension possible du schéma polygonal en 3D.
Après avoir étudié les invariants topologiques numériques que sont la caractéristique d’Euler-Poincaré et les nombres de Betti, et un invariant non numérique mais limité aux surfaces, le schéma polygonal canonique, l’étape suivante était d’étudier les groupes d’homologie. Afin d’attaquer ce problème de manière progressive, nous l’avons tout d’abord étudié en 2D dans le cas des surfaces fermées, orientables ou non [DPF06], puis nous avons étendu ce premier travail aux subdivisions orientables 3D [DPF08]. La généralisation en nD de ces travaux est en cours de réalisation.
Pour calculer les groupes d’homologie d’une 2G-carte, le principe est similaire au calcul du schéma polygonal réduit de la section précédente. Il consiste à simplifier une 2G-carte fermée, qui représente donc une surface, dans une représentation minimale tout en préservant son homologie. L’ensemble des arêtes de la 2G-carte minimale obtenue est l’ensemble des générateurs du premier groupe d’homologie de la surface initiale. L’approche utilisée est similaire à l’algorithme présenté dans [KMS98]. Mais la méthode présentée dans ce papier peut ne pas aboutir à une représentation minimale. Nous résolvons ce problème par l’utilisation de l’opération de décalage d’arête qui garantit, comme nous avons vu dans la section précédente, que l’objet obtenu soit minimal. La principale différence avec le schéma polygonal est que nous n’obtenons pas de représentation canonique mais nous limitons à l’équivalent du schéma polygonal réduit.
Le principe de la méthode présentée Algorithme 6.27 est de commencer par supprimer les arêtes de degré deux et les arêtes pendantes jusqu’à obtenir une 2G-carte composée d’une seule face, puis par supprimer les sommets de degré deux, en utilisant au préalable le décalage d’arête, jusqu’à obtenir une 2G-carte composée d’un seul sommet (le nombre d’arêtes étant alors fixé par la caractéristique d’Euler-Poincaré de la surface).
- Entrées : Une 2G-carte G fermée.
- Résultat : La simplification de G dans sa forme minimale.
1.
Pour chaque arête a de G faire
Si a est de degré 2 alors
Supprimer a;
Sinon Tant que a est une arête pendante faire
a′ ← une arête adjacente à a;
Supprimer a; a ← a′;
2.
Pour chaque sommet s de G faire
Si s est de degré 2 alors
Supprimer s;
Sinon Si il existe une arête a non-boucle incidente à s alors
Décaler toutes les arêtes incidentes à s sauf a;
Supprimer s;
Figure 6.27: Algorithme : Simplification d’une 2G-carte dans sa forme minimale.
Lors de la première étape de l’algorithme, les arêtes sont supprimées dans n’importe quel ordre. Pour les arêtes de degré deux, deux faces distinctes sont fusionnées. Les autres arêtes sont de degré un. Les arêtes pendantes doivent être supprimées, et les autres doivent être conservées car leur suppression entraînerait la déconnexion d’une face.
Lorsqu’une arête pendante a est supprimée, nous devons éventuellement re-traiter l’arête incidente à a. En effet, lorsque a est l’extrémité d’un chemin d’arêtes pendantes, sa suppression fait que l’arête précédente du chemin devient pendante et doit être supprimée (alors qu’avant la suppression de a, cette arête n’était pas pendante et devait être conservée). Ce traitement doit être itéré tant que l’arête courante est supprimée.
Lors de la seconde étape de l’algorithme, nous supprimons les sommets pour obtenir la représentation minimale composée d’un seul sommet. Chaque sommet de degré deux est supprimé. Pour les autres sommets s (de degré supérieur à deux), nous devons tester s’il existe une arête a non-boucle incidente à s. Si c’est le cas, le sommet peut-être supprimé après avoir décalé les arêtes différentes de a sur un autre sommet. Sinon, c’est que nous avons obtenu la représentation minimale de la surface avec un seul sommet incident uniquement à des boucles, et le sommet ne doit pas être supprimé.
Nous pouvons voir Figs. 6.28 et 6.29 deux exemples de cartes minimales : le premier exemple est obtenu à partir d’une 2G-carte représentant un tore à deux trous, et le second à partir d’une 2G-carte représentant une bouteille de Klein. Nous montrons dans ces deux exemples la 2G-carte initiale, celle obtenue à la fin de la première étape de suppression des arêtes, puis la 2G-carte finale qui est la représentation minimale. Dans le premier cas, cette G-carte est composée d’une face, quatre arêtes et d’un sommet : la caractéristique d’Euler-Poincaré est égale à moins deux. Dans le second cas, la G-carte est composée d’une face, de deux arêtes, et d’un sommet : la caractéristique d’Euler-Poincaré est égale à zéro.
[a][b]
[c]
Figure 6.28: Un exemple de G-carte minimale d’un tore à deux trous. (a) La 2G-carte initiale. (b) La G-carte obtenue après les suppressions d’arêtes. (c) La G-carte obtenue après les suppressions de sommets. Les brins en noirs appartiennent à l’orbite ⟨α0∘α1⟩(b).
[a][b]
[c]
Figure 6.29: Un exemple de G-carte minimale de la bouteille de Klein. (a) La 2G-carte initiale. (b) La G-carte obtenue après les suppressions d’arêtes. (c) La G-carte obtenue après les suppressions de sommets. Les brins en noirs appartiennent à l’orbite ⟨α0∘α1⟩(b).
Pour tester le degré d’une arête, nous utilisons à nouveau des arbres union-find [Tar75] (de manière similaire au calcul du niveau 2 présenté Section 4.4.2 page ??). Nous initialisons ces arbres avant de commencer les simplifications en associant un arbre différent à chaque face de la G-carte. Lors de la suppression d’une arête incidente à deux faces distinctes, nous fusionnons les deux arbres associés (face(d) et face(β2(d))). De ce fait, tester si une arête est de degré un (c-à-d incidente deux fois à la même face) se fait simplement en testant si find(d)=find(β2(d)), et la complexité amortie de ce test peut-être considéré en temps constant.
Pour montrer la validité de notre algorithme, nous avons prouvé que l’homologie est préservée par les opérations utilisées, et que la G-carte obtenue est minimale (cf. [DPF06]). Pour montrer que l’homologie est préservée, nous avons fait un parallèle entre l’opération de suppression d’arête et l’opération de réduction utilisée dans [KMS98], pour laquelle les auteurs ont prouvé que l’homologie était préservée. La preuve que la G-carte est minimale s’effectue par contradiction en supposant qu’elle est composée de plus d’un sommet, ce qui contredit le fait que toute les arêtes non boucles ont été supprimées.
De plus, les arêtes de la G-carte résultante de notre algorithme sont les générateurs du premier groupe d’homologie (sauf dans le cas particulier de la sphère où la 2G-carte minimale est composée d’une face, d’une arête et de deux sommets alors qu’il n’y a pas de générateur du premier groupe d’homologie). En effet, ces arêtes sont des cycles car ce sont toutes des boucles et donc leur bord est nul. De plus, nous pouvons distinguer les générateurs libres des générateurs de torsions. Pour cela, nous orientons la face de la G-carte obtenue, en marquant les brins de l’orbite <α0 ∘ α1>(b) où b est un brin quelconque de la G-carte. Pour chaque arête de la G-carte désignée par un de ses brins b, si b et α2(b) sont tous les deux marqués, le générateur associé à cette arête est de torsion, sinon il est libre. Dans l’exemple de la Fig. 6.5.1, nous pouvons vérifier que les deux générateurs sont libres car il n’existe pas de brin b marqué avec α2(b) également marqué. Par contre dans l’exemple de la Fig. 6.5.1, nous pouvons observer qu’un générateur est libre et que l’autre est de torsion.
Nous avons étendu l’algorithme précédent pour calculer les générateurs des groupes d’homologie d’un objet 3D orientable, c’est à dire un objet 3D bordé d’une ou plusieurs surfaces orientables.
Nous nous sommes pour cela inspiré du travail présenté dans [DG98] qui étudie l’homologie des variétés 3D. Ils montrent deux résultats que nous utilisons par la suite : (1) Pour un objet X bordé par j+1 surfaces s0,...,sj, où s0 est la surface externe de X, alors l’ensemble {s1,...,sj} est une base du deuxième groupe d’homologie H2(X) ; (2) les générateurs longitudinaux de s0 plus les générateurs latitudinaux de {s1,...,sj} forment une base du premier groupe d’homologie H1(X). Intuitivement, pour une surface bordant un objet, un générateur est longitudinal s’il «entoure» un tunnel de l’objet (donc «du vide» pour l’objet), et il est latitudinal sinon (et dans ce cas il «entoure» de «la matière» de l’objet) (cf. [DG98] pour les définitions précises).
Sur l’exemple de la Fig. 6.5.2, la surface externe s0 borde un tore à trois tunnels. Cette surface à donc six générateurs : trois longitudinaux, chacun entourant un tunnel du tore, et trois latitudinaux reliant ces trois premiers générateurs (non représentés). La surface bordant la cavité torique est composée de deux générateurs : un longitudinal entourant le tunnel du tore (non représenté) et un latitudinal entourant le tunnel du complémentaire du tore. L’ensemble des générateurs du premier groupe d’homologie est composé des trois générateurs longitudinaux de la surface externe plus le générateur latitudinal de la cavité torique. Il faut noter que le premier groupe d’homologie de la sphère est trivial, donc il n’y a pas de générateur dans ce cas.
[a][b]
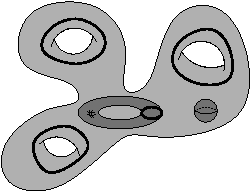
Figure 6.30: (a) Un objet 3D ayant trois tunnels et deux cavités. (b) Le générateur latitudinal de la cavité torique, et les trois générateurs longitudinaux de la surface externe de l’objet forment une base du premier groupe d’homologie de l’objet.
Le principe de l’Algorithme 6.31 consiste, comme l’algorithme précédent dans le cas 2D, à simplifier la 3G-carte en utilisant les opérations de suppression tout en préservant l’homologie de la 3G-carte.
- Entrées : Une 3G-carte G décrivant une subdivision orientable, avec chaque cellule homéomorphe à une boule topologique
- Résultat : La subdivision minimale homologue à G
1.
Pour chaque face f de G faire
Si le degré de f est 2 alors
Supprimer f;
Sinon Si f est une face pendante alors
empiler(P,f);
Faire
f ← dépiler(P);
empiler dans P toute les faces pendantes incidentes à f;
Supprimer f;
Tant que non vide(P);
Sinon Marquer f comme face fictive;
2. Supprimer toutes les faces fictives;
3. Marquer la surface externe;
4. Calculer les générateurs H1 de chaque surface;
5.
Si la surface externe est une sphère alors
ext ← la seule arête de la surface externe;
Sinon Pour une arête sur deux e de la surface externe faire
Insérer une face fictive incidente à e;
ext ← e;
Pour chaque surface interne s faire
Si s est une sphère alors
int ← la seule arête de s;
Sinon Pour une arête sur deux e de s faire
Insérer une face fictive incidente à e;
int ← e;
Insérer une face fictive face entre int et ext;
Figure 6.31: Algorithme : Simplification d’une subdivision 3D dans sa forme minimale.
Nous simplifions progressivement la subdivision d’un objet 3D dans lequel chaque cellule est initialement homéomorphe à une boule, en utilisant les opérations de suppression par dimension décroissante. Tout d’abord nous supprimons des faces tout en conservant les volumes homéomorphes à des boules. Pour cela, nous gardons des faces fictives (qui sont l’extension des arêtes fictives). Ces faces sont de degré un (c-à-d incidentes deux fois au même volume) et non pendantes. À la fin de cette étape nous obtenons une 3G-carte composée d’un seul volume. Ensuite, nous pouvons nous ramener au cas 2D présenté section précédente, mais nous devons pour cela supprimer les faces fictives. En effet, après cette suppression nous obtenons un ensemble de surfaces 2D et nous pouvons utiliser l’Algorithme 6.27 pour chacune d’elle, ce qui nous donne un ensemble de 2G-cartes minimales. Pour reconstruire la 3G-carte minimale correspondante à l’objet initial, nous insérons les faces fictives préalablement supprimées afin de rendre la 3G-carte connexe et le volume homéomorphe à une boule. Ces faces correspondent aux cellules implicites définies Section 6.3.1 pour le calcul des nombres de Betti.
Nous détaillons maintenant plus précisément chaque étape de l’algorithme de simplification. La première étape (ligne 1) consiste à supprimer toutes les faces de degré deux et toutes les faces pendantes jusqu’à obtenir un seul volume homéomorphe à une boule. Le principe est similaire à l’algorithme 2D, où lorsqu’une face pendante est supprimée, nous devons re-considérer les faces adjacentes pour traiter le cas où elles deviennent à leur tour pendantes. Durant cette étape, nous marquons les faces fictives (qui sont des faces de degré un non pendantes). À la fin de cette étape, nous obtenons une 3G-carte composée d’un seul volume homéomorphe à une boule, des faces réelles (composées de brins 3-libres) et des faces fictives (composées de brins non 3-libres).
La Fig. 6.5.2 montre un exemple de résultat obtenu à la fin de cette première étape. Nous pouvons vérifier sur cet exemple que les faces fictives sont de deux types différents : celles qui bouchent des tunnels, et celles qui relient entre elles différentes surfaces pour garder la carte connexe.
[a][b]
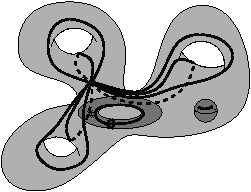
La deuxième étape de l’algorithme (à partir de la ligne 2) va travailler sur chaque surface de l’objet. Pour cela, nous supprimons chaque face fictive, ce qui va déconnecter les différentes surfaces qui pourront être considérées séparément, et marquons la surface externe. La distinction entre la surface externe et les autres surfaces est nécessaire pour calculer les générateurs H1, car pour la surface externe nous devons considérer les générateurs longitudinaux tandis que pour les autres surfaces nous devons considérer les générateurs latitudinaux. Pour marquer la surface externe, nous devons trouver un brin de départ (par exemple le brin associé à la plus petite coordonnées géométrique), puis parcourir la surface en utilisant l’orbite ⟨α0,α1,α2⟩ à partir de ce brin.
L’étape d’après (ligne 4) consiste à calculer les générateurs H1 de chaque surface de manière indépendante. Nous utilisons pour cela l’algorithme 2D présenté section précédente. En effet, même si nous travaillons sur une 3G-carte, tous ses brins sont 3-libres ce qui nous permet de considérer chaque composante connexe comme une 2G-carte.
À la fin de cette étape, nous avons obtenu la représentation minimale de chaque surface. Cette représentation est composée d’une face, une arête et deux sommets pour une sphère, et d’une face, 2k arêtes et un sommet pour un tore à k trous. Nous devons maintenant reconstruire la subdivision minimale de l’objet 3D. C’est l’objet de la dernière étape de l’algorithme (à partir de la ligne 5) qui va ajouter des faces fictives pour reconstruire une 3G-carte connexe, et composée d’un seul volume homéomorphe à une boule.
Pour cela, nous insérons une face fictive entre ext, un brin de la surface externe, et un brin de chaque surface interne, ce qui rend la 3G-carte connexe (nous ne différencions pas ici les générateurs latitudinaux et les longitudinaux car topologiquement ils ont le même rôle et donc cette distinction n’intervient pas pour le calcul des groupes d’homologies. Nous reviendrons par contre sur cette distinction qui intervient pour plonger les générateurs). Nous insérons également une face fictive pour boucher chaque tunnel. Cela se fait en insérant une face pour un brin sur deux de chaque surface. En effet, chaque arête d’un tore à k trous est une boucle, et il y a 2k arêtes. En insérant k faces fictives le long de ces boucles, nous bouchons bien chaque tunnel et obtenons un volume homéomorphe à une boule (cf. Fig. 6.5.2).
[a][b]
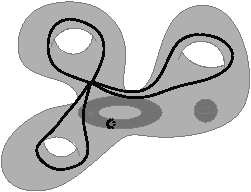
Figure 6.33: (a) La G-carte minimale obtenue à la fin de l’algorithme (représentation partielle, les faces fictives liant la surface externe et les surfaces internes ne sont pas représentées). Cette carte est homologue à la subdivision initiale. (b) Les générateurs H1 sont composés de toutes les arêtes non-incidentes à une face fictive, et non-incidentes à une sphère.
À la fin de l’algorithme, nous obtenons une carte où chaque cellule est homéomorphe à une boule. Cette propriété est nécessaire afin de prouver que la G-carte est homologue à l’objet initial. De plus, cette carte est composée de j+1 faces réelles, une pour chaque surface de la subdivision initiale, et elle contient directement les générateurs des groupes d’homologie :
Comme en 2D, la 3G-carte obtenue est homologue à l’objet initial, et permet de calculer directement les générateurs des groupes d’homologie de l’objet initial par une simple caractérisation des cellules. De plus, ce principe de simplification par dimension décroissante est intéressant dans le but d’étendre cette méthode en dimension quelconque.
Nous prouvons la validité de notre méthode en montrant que l’homologie de l’objet est préservée durant les simplifications, et que les générateurs de l’homologie peuvent être directement obtenus. Ces preuves reposent principalement sur les travaux de [KMS98] et de [DG98] (cf. [DPF08] pour ces preuves). Pour cela, nous faisons le lien entre l’opération de réduction dans les complexes simpliciaux et notre opération de suppression de face, et utilisons les travaux de [KMS98] qui montrent que ajouter une face le long de chaque générateur latitudinal coupe le volume correspondant en un objet homéomorphe à une boule. Pour la caractérisation directe des générateurs, nous utilisons les deux propriétés énoncées en début de ce chapitre et provenant de [DG98]. Pour H2(X), nous récupérons l’ensemble des surfaces internes, et pour H1(X) les générateurs longitudinaux de la surface externe, et les générateurs latitudinaux des surfaces internes. Pour distinguer les deux types de générateurs, nous utilisons les faces fictives. En effet, les arêtes incidentes aux faces fictives n’appartient pas aux générateurs de H1(X) par construction. De ce fait, nous obtenons une caractérisation simple des arêtes appartenant aux générateurs du groupe d’homologie H1(X) qui est combinatoire, et qui est plus simple que la méthode utilisée dans [DG98] et consistant à utiliser le nombre de liaisons et à perturber les générateurs.
L’Algorithme 6.31 permet de calculer la 3G-carte minimale homologue à la subdivision initiale, ce qui nous permet de calculer directement les générateurs des groupes d’homologie de l’objet. Mais il n’est pas directement possible de retrouver le lien entre ces générateurs et les cellules de la subdivision initiale pour H1.
C’est par contre possible pour H2, car chaque face réelle de la carte minimale va fournir un brin de départ pour une surface de la subdivision originale. Parcourir cette surface se fera ensuite simplement par un parcours de surface en sautant les brins non 3-libres, qui appartiennent forcément aux faces fictives
Pour les générateurs de H1, la difficulté concerne la dernière étape de l’algorithme qui insère des faces fictives en prenant une arête sur deux des surfaces, sans propriétés particulières sur ces arêtes. Cela suffit pour le calcul des groupes d’homologie car ces arêtes jouent topologiquement des rôles identiques, mais cela pose problème pour le lien avec la subdivision initiale car les plongements de ces arêtes n’ont plus des rôles équivalents (il faut conserver les arêtes entourant uniquement du vide par rapport à l’objet). Pour résoudre ce problème, il suffit d’ajouter un test supplémentaire dans l’Algorithme 6.31 :
Avec ces deux modifications, les générateurs H1 peuvent maintenant être plongés sur la G-carte initiale. Mais pour cela, il faut conserver lors des opérations de suppression d’arêtes et de décalage d’arête un lien entre les arêtes modifiées et les arêtes de la subdivision initiale, de manière similaire à ce que nous avons présenté au chapitre 5 pour les chemins de connexion.
Dans ce chapitre, nous avons présenté plusieurs méthodes permettant de calculer différents invariants topologiques pour les cartes : un algorithme de calcul de la caractéristique d’Euler-Poincaré, le calcul des nombres de Betti, avec une version de mise à jour locale lors des opérations de suppression, le schéma polygonal canonique d’une surface, et les groupes d’homologie d’une surface fermée, et d’un volume orientable fermé.
Ces différentes méthodes ont toutes comme point commun d’être en lien avec les opérations de suppression et contraction, qui sont utilisées dans des cadres différents, mais toujours en contrôlant l’évolution des caractéristiques topologiques. Ce sont ces opérations de simplification qui nous ont permis de proposer des algorithmes efficaces permettant de mettre à jour les invariants topologiques de manière locale lors de ces opérations.
Par contre nos travaux ne sont pas tous au même niveau concernant les différents invariants topologiques. En effet, notre objectif global est de fournir des outils génériques autour des cartes, et nous avons pour le moment restreint le calcul des nombres de Betti et des générateurs des groupes d’homologie à une sous-classe d’objets (2D ou 3D orientable fermé).
Cela ouvre donc directement des perspectives à ce chapitre qui sont l’extension des méthodes proposées en dimension quelconque et à des objets quelconques (ouverts ou non, orientables ou non). Pour cela, nous devons étudier plus précisément la notion de face fictive, et plus généralement en dimension n de cellule fictive, pour éviter l’étape de déconnexion utilisée dans l’algorithme de calcul des générateurs de l’homologie 3D. En effet, en utilisant un procédé similaire à celui du décalage des arêtes en 2D, nous devrions pouvoir éviter cette étape en décalant les faces fictives. Cela aurait l’avantage de ne pas avoir perdu une information durant la déconnexion (la différence entre les générateurs longitudinaux et latitudinaux), et cela permettrait également plus facilement de faire le lien entre la carte minimale et la représentation initiale de la subdivision.
Pour proposer une méthode générale de calcul des groupes d’homologie en nD, nous avons défini dans [APDL09] un opérateur de bord en dimension quelconque, qui est l’étape préalable à la définition directe de l’homologie cellulaire. De plus, nos travaux actuels ont principalement porté sur l’utilisation des opérations de suppression, et il serait également intéressant d’étudier le lien avec l’opération de contraction. Une autre piste que nous avons pour le moment étudiée en 2D dans [PIH+07, PIK+09] est l’utilisation d’une pyramide de cartes pour guider les calculs des groupes d’homologie. L’idée consiste à construire une pyramide, en préservant l’homologie des objets manipulés, puis de manière un peu similaire aux algorithmes de mise à jour locaux, à calculer les générateurs de l’homologie sur le niveau au sommet de la pyramide, puis à propager ces générateurs de niveau en niveau jusqu’à la base. Ce type de technique a l’avantage d’effectuer le calcul initial sur un niveau contenant très peu de cellules (proche d’une carte minimale), mais également de simplifier la propagation en la découpant en plusieurs petites étapes. Un autre avantage de ce type de technique est qu’il est possible de déformer la géométrie des générateurs lors de leurs projection de niveau en niveau, en garantissant bien évidemment la préservation de leur topologie.
Nous allons maintenant nous intéresser aux applications des modèles et des opérations que nous avons présentés tout au long de ce mémoire. Nous avons principalement deux champs applicatifs privilégiés qui sont la modélisation géométrique et le traitement d’images. Dans les deux cas, nos préoccupations centrales tournent autour de la topologie et de son apport dans les différentes opérations.


