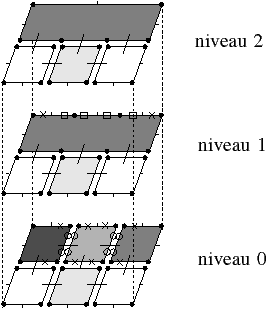
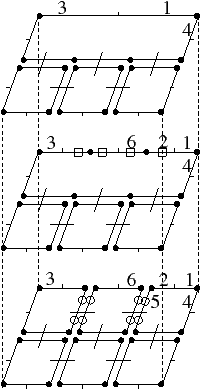
| Figure 5.1: Exemple de pyramide de 2G-cartes composée de trois niveaux. Les brins 0-supprimés (resp. 1-supprimés) sont marqués par □ (resp. ∘); les brins voisins d’une cellule supprimée sont marqués par ×. |



Dans ce chapitre, nous étudions une extension des cartes afin de décrire une hiérarchie de partitions, ainsi que les liens entre ces partitions : les pyramides de cartes. Ce type de représentation permet par exemple de décrire un objet à différentes résolutions, ou de manipuler différentes subdivisions d’un même objet, chaque subdivision pouvant correspondre à une certaine description sémantique.
Il existe de nombreux travaux ayant étudié des représentations hiérarchiques. Comme pour les modèles de représentation d’images présentés au chapitre précédent, de nombreuses recherches ont tout d’abord porté sur l’utilisation de graphes pour définir des pyramides de graphes d’adjacence [Mee89, MMR91, JM92, Jol03], avant d’être étendus aux pyramides de graphes duaux [WK94, KM95, Kro95]. Par la suite, compte-tenu des avantages des cartes combinatoires par rapport aux graphes, des recherches ont porté sur la définition des pyramides de cartes combinatoires [BK01, BK02, BK03a] mais uniquement en 2D. Il faut également citer d’autres travaux en modélisation géométrique, où différentes structures ont été proposées, et notamment le modèle simplicial multi-résolution [dFPM97], ou des modèles ad hoc basés sur les cartes généralisées [Lev99, Gui00, Fra04]. Ces différentes structures hiérarchiques ont soit l’inconvénient de ne pas représenter toutes les informations topologiques (cellules, incidences et adjacences), soit d’être définies uniquement en 2D, soit d’être définies spécifiquement pour un domaine précis.
Pour ces raisons, nous avons étudié la définition d’une structure de données qui soit à la fois générique, c’est-à-dire pouvant s’adapter à différents domaines d’utilisation et en dimension quelconque, et complète, c’est-à-dire qu’elle représente toutes les cellules et relations d’incidence et d’adjacence : c’est ce que nous avons appelé les pyramides généralisées. Nous avons ensuite étudié les propriétés de cette structure de données, le lien entre ses différents niveaux, et différentes représentations possibles. Ce travail est le résultat de la thèse de Carine Grasset-Simon [Sim06] et a été présenté dans [SDL05a, SDL05b, SDL06].
L’organisation de ce chapitre est la suivante. Nous commençons Section 5.1 par introduire et définir les pyramides généralisées. Puis Section 5.2 nous présentons les orbites généralisées, une extension des orbites entre deux niveaux non nécessairement consécutifs d’une pyramide. Enfin, Section 5.3, nous définissons trois représentations différentes de ces pyramides. Ces trois représentations sont équivalentes, mais sont plus ou moins compactes en mémoire, au détriment bien entendu d’une représentation plus ou moins explicite des différentes informations. Enfin nous concluons cette partie et donnons des perspectives Section 5.4.
Une pyramide de cartes généralisées, appelée pyramide généralisée, est une structure hiérarchique composée d’une séquence de nG-cartes, où chaque niveau est une réduction du niveau précédent obtenue par l’application des opérations de suppression et contraction de cellules.
Nous présentons Def. 71 la définition des pyramides généralisées basée sur les opérations de contraction et suppression.
Chaque nouveau niveau de la pyramide est obtenu par simplification du niveau précédent en supprimant et contractant certaines cellules. Nous conservons ici les notations introduites à la Section 3.2 lors de la définition de l’opération de suppression et contraction simultanées, en ajoutant un exposant pour indiquer le niveau concerné dans la pyramide. De ce fait, ∀ l: 0 ≤ l <m et ∀ i: 0 ≤ i ≤ n, nous notons Sil et Cil les ensembles de i-cellules du niveau l qui sont respectivement supprimées et contractées, et BVil l’ensemble des brins survivants du niveau l, i-voisins de i-cellules supprimées ou contractées.
Par définition de l’opération de suppression et contraction simultanées (cf. Def. 53 page ??), ces cellules doivent vérifier les conditions suivantes :
Un exemple de pyramide de 2G-cartes est donnée Fig. 5.1.1.

Figure 5.1: Exemple de pyramide de 2G-cartes composée de trois niveaux. Les brins 0-supprimés (resp. 1-supprimés) sont marqués par □ (resp. ∘); les brins voisins d’une cellule supprimée sont marqués par ×.
Suite à cette définition des pyramides généralisées, il est facile de prouver qu’un brin ne peut disparaître qu’une seule fois au cours de la construction de la pyramide, c’est-à-dire à un seul niveau de la pyramide et suite à une seule opération : par la suppression ou la contraction d’une cellule. Nous parlons de brin survivant au niveau l pour un brin qui n’appartient pas à une cellule contractée ou supprimée de ce niveau, et notons BSl pour l’ensemble des brins survivants du niveau l. Ces brins sont reliés par ϕl aux brins de BSl+1. Plus formellement, ϕl est la bijection ϕl:BSl → Bl+1 induite par l’opération de suppression et contraction simultanées utilisée lors de la définition du niveau l+1 à partir du niveau l. Cette bijection est la relation successeur existant entre les brins survivants du niveau l de la pyramide et les brins du niveau l+1. De plus, la bijection inverse (ϕl)−1 est la relation prédécesseur existant entre les brins du niveau l+1 et les brins survivants du niveau l. Nous notons nivb le dernier niveau dans lequel le brin b existe. Si b appartient à une cellule supprimée ou contractée à un niveau l<m, alors nivb=l, sinon (b est survivant à chaque niveau), nivb=m.
Après avoir défini la notion de pyramide, il est nécessaire d’étudier le moyen de retrouver les informations d’un niveau en propageant les informations des niveaux précédents. Ces notions sont liées aux chemins de connexions («connecting walks» en anglais) initialement définis par Brun et Kropatsch dans le cadre des pyramides combinatoires (cf. [BK01]) en 2D. Intuitivement, un chemin de connexion entre deux brins reliés par αi au niveau j permet de retrouver les brins du niveau j−1 parcourus lors de la redéfinition de αi par l’opération de suppression et contraction simultanées. La définition de ces chemins peut ensuite être étendue entre deux niveaux non consécutifs. Mais cette notion n’est pas suffisante pour manipuler les informations au sein d’une pyramide. En effet, une information est souvent associée à une orbite d’un certain niveau (par exemple les coordonnées d’un point associées à une orbite sommet). De ce fait, nous nous sommes intéressés à l’extension de la notion d’orbite permettant de retrouver tout les brins d’un niveau inférieur qui composent une orbite d’un niveau donné : c’est la notion d’orbite généralisée. Cette notion permet de propager les informations associées aux orbites d’un niveau inférieur à n’importe quel niveau de la pyramide.
Un chemin de connexion, défini entre deux niveaux consécutifs de la pyramide, est une séquence de brins du niveau inférieur séparant deux brins liés par un αi au niveau supérieur (cf. exemple Fig. 5.1.2). La liaison entre deux brins d’un même niveau est, par définition de l’opération de suppression/contraction simultanée, déduite d’une succession de liaisons du niveau précédent, effectuées en tenant compte de l’état des brins parcourus, à savoir supprimé, contracté ou survivant. Ainsi, la définition du chemin de connexion entre deux niveaux consécutifs a et a+1, pour un brin b donné et pour une involution αi donnée, reprend les termes de la définition de l’involution αia+1. Nous notons Ch(i,a,d)(b) le chemin de connexion défini entre les niveaux a et d (a ≤ d), pour l’involution αi et pour le brin b ∈ Bd.
Les chemins de connexion peuvent être définis de manière récursive (cf. Def. 72) ou itérative (cf. Def. 73). Dans les deux cas, le principe de base est similaire : il consiste à regarder l’état du brin courant, et selon les cas (supprimé, contracté, survivant) à utiliser la liaison en relation avec l’opération correspondante, ou à changer de niveau pour récupérer les informations du niveau précédent.
L’idée principale de la définition récursive repose sur le fait qu’un chemin de connexion entre les niveaux a et d est une concaténation de sous-chemins entre les niveaux a et d−1 séparant les brins du niveau d−1 qui relient b et b′ et qui appartiennent à des cellules supprimées ou contractées au niveau d−1 (étant donné deux chemins C1 et C2, nous notons (C1,C2) le chemin obtenu par concaténation de C1 et C2).
| i si u est impair, |
| i+1 si u est pair et bu ∈ Sid−1, |
| i−1 si u est pair et bu ∈ Cid−1. |
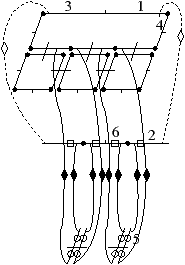
Comme nous pouvons le voir sur la Fig. 5.2, le chemin de connexion Ch(0,0,2)(1), défini entre les niveaux 0 et 2 et reliant les brins 1 et 10 correspond à la concaténation des sous-chemins Ch(0,0,1)(1)=(2), Ch(1,0,1)(2)=(3,4,5), Ch(0,0,1)(5)=(6), Ch(1,0,1)(6)=(7,8,9) et Ch(0,0,1)(9)=(10) composant respectivement les liaisons existant entre les brins séparant les brins 1 et 10 au niveau 1.
[a][b]
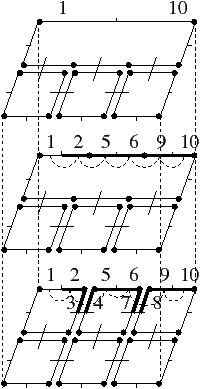
Figure 5.2: Chemins de connexion. La pyramide considérée est celle de la Fig. 5.1.1. (a) Exemples de chemin entre deux niveaux consécutifs : les brins des chemins de connexion Ch(1,0,1)(2) et Ch(1,0,1)(6) sont dessinés en gras au niveau 0 de la pyramide. Ces brins se situent respectivement entre les brins 2 et 5, et entre les brins 6 et 9 où 5 = 2 α11 et 9 = 6 α11 : Ch(1,0,1)(2) = (3,4,5) et Ch(1,0,1)(6) = (7,8,9). (b) Exemple de chemin entre deux niveaux non consécutifs : les brins du chemin de connexion Ch(0,1,2)(1) sont dessinés en gras au niveau 1 de la pyramide. Ces brins se situent entre les brins 1 et 10 où 10 = 1 α02 : Ch(0,1,2)(1) = (2,5,6,9,10). Les brins du chemin de connexion Ch(0,0,2)(1) sont dessinés en gras au niveau 0 de la pyramide : Ch(0,0,2)(1)=(2,3,4,5,6,7,8,9,10).
Une autre manière de définir la notion de chemin de connexion est de le faire itérativement et non récursivement. L’idée repose sur le fait que connaissant l’état du brin courant (supprimé ou contracté) et l’involution ayant permis d’arriver sur ce brin, il est possible de déduire la prochaine involution du chemin.
En se plaçant entre deux niveaux consécutifs a et a+1, nous utilisons les propriétés suivantes sur le chemin issu de b par αi :
Nous pouvons remarquer que par définition des i-cellules, le chemin peut parcourir différentes i-cellules, supprimées ou contractées au niveau a :
Soient bu le dernier brin du chemin qui a été découvert, et αku−1a l’involution qui a permis de le découvrir. Nous pouvons alors remarquer que :
Afin d’exprimer la prochaine involution (αku) en fonction de la dernière involution (αku−1), les quatre points précédents peuvent être reformulés de la manière suivante :
Ces quatre formules, étant donné un brin et la dernière involution, nous donnent la prochaine involution, et donc le prochain brin du chemin. Les constatations précédentes, réalisées dans le cas d’un chemin de connexion défini entre deux niveaux consécutifs, peuvent être généralisées dans le cas où nous considérons un chemin entre deux niveaux quelconques, ce qui nous permet ainsi de déduire la définition itérative suivante :
| ||||||
| ||||||
Les chemins de connexion vérifient différentes propriétés prouvées dans [Sim06] :
D’autre part, de la même manière qu’une involution liant deux brins est symétrique, le chemin de connexion liant deux brins est «réversible». En effet, soit C un chemin de connexion liant les brins b et b αid auquel est ajouté b en premier élément. La séquence de brins inverse de C correspond au chemin de connexion liant b αid à b auquel est ajouté b αid en premier élément. D’autre part, si deux ensembles connectants ouverts ne sont pas égaux alors ils n’ont aucun brin en commun. De plus, les deux définitions des chemins de connexion donnent directement deux algorithmes permettant de parcourir ces chemins, le premier récursif basé sur la Def. 72, et le second itératif basé sur la Def. 73.
Nous notons DBC(i,a,d)(b) le dernier brin du chemin de connexion Ch(i,a,d)(b).
Étant donné un chemin de connexion Ch(i,a,d)(b), nous pouvons déduire deux ensembles de brins : l’ensemble connectant ouvert Ech(i,a,d)∘(b), et l’ensemble connectant fermé Ech(i,a,d)(b). Intuitivement, le premier ensemble correspond à l’ensemble des brins à l’intérieur du chemin de connexion et le second correspond à l’ensemble des brins du chemin, extrémités incluses.
| ∅ si Ch(i,a,d)(b)=() |
| Ech(i,a,d)∘(b)⋃{b,b′} sinon, où b′ =DBC(i,a,d)(b) |
Tout niveau d’une pyramide généralisée est construit à partir du niveau précédent en effectuant des suppressions ou contractions de cellules. Ainsi, toute cellule supprimée ou contractée à un niveau a une incidence directe sur la construction des cellules et plus généralement des orbites composant le niveau suivant. Si un chemin de connexion Ch(i,d−1,d) permet de tenir compte des modifications occasionnées par la disparition de i-cellules situées entre deux i-cellules survivantes en les parcourant partiellement, il ne permet pas de tenir compte des i-cellules disparues non situées entre deux i-cellules survivantes.
Nous pouvons voir Fig. 5.3 le problème que cela occasionne lorsque les chemins de connexion sont utilisés pour retrouver par exemple les faces d’un niveau d−1 qui ont fusionnées en une seule face F au niveau d. Nous retrouvons seulement les faces qui sont incidentes au «bord» de la face F.
[a][b]
[c]
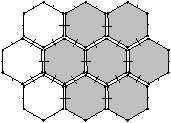
Figure 5.3: (a) Les niveaux d−1 et d d’une pyramide de 2G-cartes. Le niveau d est obtenu à partir du niveau d−1 par suppression des quatorze arêtes marquées par ∘. En grisé la face F pour laquelle nous cherchons l’ensemble des faces du niveau d−1 qui ont fusionné pour former F. (b) En grisé, les six faces obtenues en utilisant les chemins de connexion à partir des brins survivants. (c) En grisé, l’ensemble des sept faces que nous souhaiterions retrouver et qui correspond à l’ensemble des faces qui ont été fusionnées pour former F.
En effet, comme nous pouvons le voir dans la Fig. 5.4 qui détaille les différents chemins de connexion utilisés, les chemins de connexion Ch(1,d−1,d) permettent de découvrir les arêtes a à h situées entre deux arêtes survivantes, mais pas les arêtes i à n non situées entre deux arêtes survivantes.
[a][b]
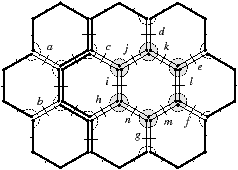
Figure 5.4: Niveau d−1 de la pyramide de la Fig. 5.1.3 où le niveau d est obtenu par suppression des arêtes a à n. Le parcours de chaque chemin de connexion Ch(1,d−1,d) est symbolisé en pointillé, et les arêtes survivantes au niveau d sont dessinées en gras. (a) Les chemins de connexion Ch(1,d−1,d) permettent de découvrir partiellement les arêtes a à h situées entre deux arêtes survivantes. Mais ces chemins ne permettent pas de découvrir les arêtes i à n non comprises entre deux arêtes survivantes. (b) En grisé, des chemins appliquant les mêmes règles de parcours que les chemins de connexion Ch(1,d−1,d) mais partant d’un brin supprimé n’appartenant pas à une arête découverte partiellement par un chemin de connexion Ch(1,d−1,d).
L’idée des chemins de connexion étendus est de permettre de parcourir toutes les cellules disparues entre deux niveaux consécutifs pour ainsi tenir compte de toutes les cellules étant intervenues dans la construction d’une cellule donnée. Pour cela, la notion de chemin de connexion est étendue à tout brin b de la pyramide de la manière suivante :
Les chemins de connexion étendus sont donc l’extension des chemins de connexion définis pour tout brin et non plus seulement les brins survivants. Comme les chemins non-étendus, ces chemins étendus peuvent être définis de manière récursive et de manière itérative.
| i si u est impair, |
| i+1 si u est pair et bu ∈ Sid−1, |
| i−1 si u est pair et bu ∈ Cid−1. |
| si b ∈ (Sid−1 ⋃ Cid−1) : br appartient à Bd, |
| si b ∈ (Sjd−1 ⋃ Cjd−1) avec j ≠ i : br appartient à Bd−1. |
| ||||||
| ||||||
Les chemins de connexion étendus vérifient des propriétés similaires à celles des chemins de connexion. Tout d’abord, les deux définitions, itérative et récursive, proposées pour ces chemins sont équivalentes et définissent un unique chemin à partir d’un brin. De plus, deux chemins de connexion étendus, observés entre deux mêmes niveaux sont soit disjoints soit ils ont un ou plusieurs sous-chemins consécutifs en commun.
De manière similaire aux chemins de connexion, nous notons DBCE(i,a,d)(b) le dernier brin d’un chemin de connexion étendu, et nous définissons l’ensemble connectant étendu ouvert EchE(i,a,d)∘(b), et l’ensemble connectant étendu fermé EchE(i,a,d)(b). Ces ensembles connectants étendus sont à la base de la définition des orbites généralisées.
| ∅ si ChE(i,a,d)(b)=() |
| EchE(i,a,d)∘(b)⋃{b,b′} sinon, où b′ =DBCE(i,a,d)(b) |
Dans le cadre des pyramides de graphes [MMR91] ou des pyramides combinatoires [BK03b], souvent utilisées pour stocker différentes partitions d’une même image 2D, la notion de champ récepteur («receptive field» en anglais) permet de retrouver l’ensemble des pixels qui ont été fusionnés pour former une région de l’image dans une certaine partition. De façon plus générale, un champ récepteur représente en 2D l’ensemble connexe des cellules de dimension deux (représentées par les sommets du graphe) du niveau initial qui ont été fusionnées pour former une cellule de dimension deux observée à un niveau donné de la pyramide.
Dans la pyramide de graphes de la Fig. 5.5, le champ récepteur associé au sommet s situé au troisième niveau de la pyramide est l’ensemble des sommets dessinés en noir au niveau initial. Dans le cas où cette pyramide représente une pyramide d’images, le champ récepteur correspond à l’ensemble des pixels de l’image initiale (sommets du niveau initial de la pyramide) qui composent la région observée (sommet d’un niveau supérieur de la pyramide).
[a][b]
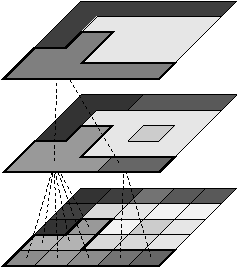
Figure 5.5: Champ récepteur dans une pyramide de graphes. (a) Pyramide de graphes avec en noir les nœuds des deux premiers niveaux qui correspondent au nœud s du troisième niveau. (b) Pyramide d’images correspondante.
Puisque les cartes généralisées ne représentent pas uniquement les cellules de plus grande dimension, mais toutes les cellules et même plus généralement toutes les orbites composant l’objet observé, il est nécessaire de pouvoir retrouver des informations quel que soit le type de cellule ou d’orbite observée. D’autre part, l’information utile n’étant pas nécessairement située au niveau initial de la pyramide, il est nécessaire de pouvoir retrouver l’information désirée dans n’importe quel niveau de la pyramide. Pour répondre à ces besoins, nous avons défini la notion d’orbite généralisée comme une extension des champs récepteurs en toute dimension, pour toute orbite, et entre deux niveaux quelconques.
Nous allons tout d’abord introduire la notion d’orbite généralisée de manière intuitive, en étudiant pour cela l’exemple de la Fig. 5.6, où l’orbite observée est l’arête l (nous parlons de cellule généralisée pour désigner l’orbite généralisée associée à une orbite correspondant à une cellule, et de sommet généralisé, arête généralisée …pour une orbite généralisée correspondant à un sommet, une arête …) :
La formation de l’arête l est alors due à :
Puisque ces arêtes sont intervenues lors de la formation de l’arête l, elles doivent toutes faire partie de l’arête généralisée associée à l’arête l. Ainsi, suivant le niveau considéré, nous obtenons les arêtes généralisées suivantes :
Plus généralement, la i-cellule généralisée associée à une i-cellule c est l’ensemble des i-cellules :
[a][b]
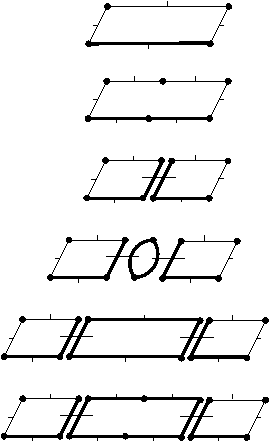
Figure 5.6: Présentation intuitive d’une orbite généralisée. (a) Pyramide de 2G-cartes comptant six niveaux obtenus par suppressions d’arêtes (∘), contractions d’arêtes (•), suppression de sommets (□) et contraction de faces (filled square). (b) À chaque niveau de la pyramide, les arêtes composant l’arête généralisée associée à l’arête l sont dessinées en gras.
L’idée principale du parcours des brins composant une orbite généralisée est d’utiliser une méthode similaire à celle mise en pratique pour parcourir les brins d’une orbite, en remplaçant l’utilisation des αi par l’utilisation des Ch(i,a,d). Par définition, une orbite est l’ensemble des brins pouvant être atteints à partir d’un brin donné en utilisant les involutions définissant l’orbite. Par exemple, l’orbite ⟨α0,α1⟩(b) qui, en 3D, correspond à l’ensemble des brins appartenant à une même face d’un même volume, est obtenue à partir du brin b en effectuant un parcours utilisant les involutions α0 et α1.
Par analogie, nous introduisons la suite ( OGi(K,a,d)(b) ) qui définit le parcours de l’orbite généralisée OG(K,a,d)(b) associée à l’orbite <>(K)d(b) du niveau d, et observée au niveau a.
| et | ∀ i: i > 0, |
| OGi(K,a,d)(b) = ∪j ∈ K ∪b′ ∈ OGi−1(K,a,d)(b) EchE(j,a,min{d, nivb′+1})(b′). |
Cette suite est croissante, bornée, et stationnaire car il existe p, 0 ≤ p ≤ |Ba|, tel que ∀ i: i ≥ p: OGi(K,a,d)(b) = OGp(K,a,d)(b). La suite ( OGi(K,a,d)(b) ) converge donc en un nombre fini d’itérations, et sa limite peut donc être considérée.
Dire que b′ est un brin de OG(K,a,d)(b) est équivalent à dire qu’il existe une suite de brins {b1, …, bq+1}, qui lie les brins b et b′ au moyen d’une succession de chemins de connexion étendus (ou d’une partie d’un chemin de connexion étendus).
Les orbites généralisées vérifient les propriétés suivantes, prouvées dans [Sim06] :
De manière générale, les orbites les plus utilisées sont les cellules. Il en est de même pour les orbites généralisées, et nous avons donc étudié plus particulièrement les propriétés des orbites généralisées associées à des cellules, que nous appelons cellules généralisées et nous notons CG(i,a,d)(b) pour la i-cellule généralisée calculée au niveau a et associée à la i-cellule du niveau d contenant le brin b.
Dans le cas où la pyramide considérée ne contient aucune suppression ni contraction de i-cellule, les i-cellules généralisées respectent une propriété particulièrement intéressante : deux i-cellules généralisées sont nécessairement disjointes ou confondues. Il faut noter que cette propriété n’est pas vérifiée dans le cas général.
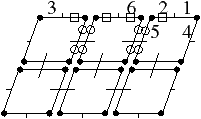
Cette propriété est illustrée dans l’exemple de la Fig. 5.7. Dans cette pyramide de 2G-cartes, il n’y a pas eu de contraction ni suppression de face. De ce fait, les faces généralisées observées dans cette pyramide sont soit distinctes, soit confondues. Les niveaux 0 et 1 sont tous les deux composés de quatre faces généralisées distinctes associées chacune à une face du niveau 2. Trois d’entre elles sont respectivement associées aux faces du niveau 2 contenant les brins 14, 15 et 16, et la quatrième correspond à deux faces généralisées confondues et respectivement associées aux faces du niveau 2 contenant les brins 1 et 13. Nous pouvons remarquer au niveau 2, que si la face grise en tant que cellule d’une subdivision est représentée dans la G-carte par deux orbites faces du fait que la G-carte ne soit plus connexe, les faces généralisées calculées à partir de ses bords sont confondues car elles utilisent les informations des niveaux précédents dans lesquels la carte était connexe.
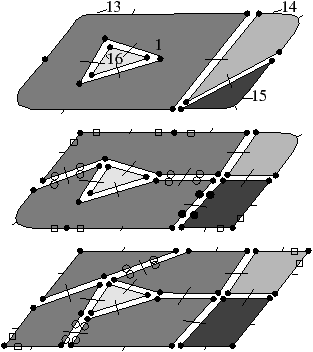
Figure 5.7: Pyramide de 2G-cartes comportant trois niveaux. Les niveaux 1 et 2 sont respectivement obtenus à partir des niveaux 0 et 1 par suppression des sommets marqués par □, suppression des arêtes marquées par ∘ et par contraction des arêtes marquées par •. Les faces généralisées associées aux orbites faces contenant les brins 1, 13, 14, 15 et 16 sont représentées à chaque niveau par différents niveaux de gris. Remarquons que les deux orbites faces contenant respectivement les brins 1 et 13 et représentant les deux bords déconnectés d’une même face sont associées à la même face généralisée. Dans cette pyramide ne comportant ni suppression ni contraction de face, les faces généralisées sont soit disjointes, soit confondues.
Une pyramide de cartes généralisées peut être représentée de façon plus ou moins explicite selon les besoins des applications. Il s’agit ici d’un problème classique de définition d’une structure de données concrète : il est nécessaire d’une part de compléter la structure en fonction des informations nécessaires pour l’application, et d’autre part de choisir en fonction des informations manipulées et des opérations utilisées, l’équilibre optimal entre information explicitement et implicitement représentées (compromis d’efficacité espace mémoire / temps de calcul).
De multiples représentations des pyramides de cartes généralisées sont possibles : nous décrivons ici trois représentations «caractéristiques» : explicite, hiérarchique et implicite. La représentation explicite correspond exactement à la définition des pyramides généralisées, chaque niveau de la pyramide est explicitement représenté ainsi que les liens entre les niveaux. La représentation hiérarchique définit les différents niveaux par un même ensemble de brins évitant ainsi une certaine redondance de l’information. Enfin, la représentation implicite est particulièrement intéressante pour le stockage sur disque puisque seul le niveau de base est explicitement représenté, les autres niveaux pouvant être déduits en conservant les opérations effectuées pour les réaliser.
La Fig. 5.8 illustre chacune de ces trois représentations dans le cas d’une pyramide de 2G-cartes. Cette pyramide est composée de trois niveaux, les deuxième et troisième niveaux étant respectivement obtenus par suppression de deux arêtes et de deux sommets.
[a][b]
[c]
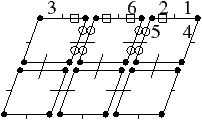
Figure 5.8: Trois représentations d’une même pyramide de 2G-cartes. (a) Représentation explicite : chaque niveau de la pyramide est explicitement représenté. Un □ (resp. ∘) marque un brin d’une 0-cellule (resp. une 1-cellule) à supprimer. (b) Représentation hiérarchique : les brins composant les différents niveaux ne sont pas dupliqués, mais toutes les involutions des différents niveaux sont représentées. Les cellules supprimées sont marquées de la même manière que dans la représentation explicite. Chaque brin est ici dessiné dans le dernier niveau de la pyramide où il existe. Quand deux brins liés par αi sont dessinés dans le même niveau, leur liaison αi est dessinée de manière usuelle. Sinon, les liaisons α01 et α00 entre deux brins de deux niveaux différents sont représentées par des lignes marquées par ◇, et les liaisons α10 par des lignes marquées par filled diamond. (c) Représentation implicite : elle est composée d’une unique G-carte correspondant au niveau initial de la pyramide. Un ∘ (resp. un □) marque un brin d’une 1-cellule du niveau 0 (resp. une 0-cellule du niveau 1) à supprimer.
La représentation explicite d’une pyramide généralisée est très proche de la définition de celle-ci. Chaque niveau de la pyramide est explicitement représenté ainsi que chaque bijection existant entre ces niveaux. Comme l’illustre la Fig. 5.9, cette représentation contient autant de cartes généralisées que la pyramide compte de niveaux, et les liaisons bijectives successeur-prédécesseur existant entre les brins de deux niveaux consécutifs sont également présentes. Ainsi, tout brin à tout niveau est lié à son prédécesseur et à son successeur, mis à part les brins du niveau initial de la pyramide qui n’ont pas de prédécesseur, et les brins disparus ou du dernier niveau de la pyramide qui n’ont pas de successeur.
niveau 0 α00 α10 α20 marque 1 2 4 1 2 1 5 2 niveau 1 α01 α11 α21 marque 1 2 4 1 2 1 6 2 S0 niveau 2 α02 α12 α22 marque 1 3 4 1
Figure 5.9: Représentation explicite de la pyramide de la Fig. 5.8. Le tableau associé précise les images des brins 1 et 2 pour chaque niveau et chaque involution.
Afin de différencier, à chaque niveau de la pyramide, les brins appartenant à une cellule supprimée ou contractée des brins survivants, deux marques sont associées à chaque brin éliminé, indiquant d’une part l’opération concernée (contraction ou suppression), et d’autre part la dimension de la cellule concernée dans l’élimination. Bien sûr, ces marques respectent les contraintes de cohérence des pyramides de G-cartes (par exemple si un brin est marqué par une marque d’opération et une marque de dimension, tous les brins de la cellule concernée possèdent les mêmes marques).
Ce type de représentation est intéressant du point de vue théorique car les différents niveaux et les relations sont plus simples à manipuler lorsqu’ils sont explicites. Il est également intéressant pour manipuler les niveaux de manière indépendante : chaque niveau étant une G-carte, il est simple de conserver un niveau en mémoire et de laisser les autres niveaux sur disque.
La représentation hiérarchique d’une pyramide généralisée est plus compacte que la représentation explicite. En effet, tenant compte de la bijection existant entre les brins survivants d’un niveau et les brins du niveau suivant, elle limite la redondance en identifiant ces deux ensembles de brins (Ba+1 = Ba − (Sa ∪ Ca), ∀ a: 0≤ a < m).
Cette représentation est composée d’un unique ensemble de brins, celui du niveau initial de la pyramide, sur lequel sont définies (éventuellement de façon partielle) les différentes involutions des différents niveaux de la pyramide. Un exemple illustrant la représentation hiérarchique d’une pyramide de 2G-cartes est donné Fig. 5.10. Dans cette représentation nous associons au brin 1 (resp. au brin 2) trois suites, une pour chaque involution α0, α1, et α2. Ainsi, la première suite indique que le brin 1 (resp. 2) est lié par α0 au brin 2 aux niveaux 0 et 1, puis au brin 3 au niveau 2 (resp. au brin 1 aux niveaux 0 et 1). Une deuxième suite indique qu’il est lié par α1 au brin 4 aux trois niveaux (resp. au brin 5 au niveau 0, et au brin 6 au niveau 1). Enfin une troisième suite indique qu’il est lié à lui-même par α2 aux trois niveaux également (resp. à lui-même aux niveaux 0 et 1). Une optimisation possible pour compacter ces informations consiste à associer à chaque brin une suite ne comportant (pour chaque involution) que les brins différents ainsi que le niveau auquel l’involution d’un brin est modifiée. Pour l’exemple de la Fig. 5.10, trois suites seront associées au brin 1. La première, correspondant à α0, ne comportera que deux éléments (0,2) et (2,3), indiquant que le brin 1 est lié par α0 au brin 2 du niveau 0 au niveau 1 inclus, puis au brin 3 à partir du niveau 2. Les deuxième et troisième suites ne comporteront chacune qu’un seul élément, respectivement (0,4) et (0,1), indiquant que le brin 1 est respectivement lié par α1 et α2 aux brins 4 et 1 à partir du niveau 0.
brin 1 marque -1.5exliaisons niveaux 0 1 2 α0 2 2 3 α1 4 4 4 α2 1 1 1
brin 2 marque S0 -1.5exliaisons niveaux 0 1 2 α0 1 1 α1 5 6 α2 2 2
Figure 5.10: Représentation hiérarchique de la pyramide de la Fig. 5.8. Les tableaux associés précisent les images par α0, α1 et α2 des brins 1 et 2 pour chaque niveau.
D’autre part, et de la même manière que pour la représentation explicite, deux marques sont associées à chaque brin éliminé : la première indique l’opération appliquée pour éliminer ce brin, la deuxième indique la dimension de la cellule concernée par l’opération.
Ce type de représentation est intéressant dans les traitements top-down où l’on commence à traiter un objet à un faible niveau de résolution avant d’éventuellement aller étudier certaines parties de manière détaillée. Il est proche du modèle proposé dans [KCB09] pour représenter des surfaces de subdivision, et de celui proposé dans [Fra04] pour représenter des bâtiments sous forme hiérarchique.
La représentation implicite est la représentation compacte d’une pyramide généralisée. Cette représentation tient compte du fait que chaque niveau est déduit du niveau précédent, et peut donc être construit à partir du niveau initial si la séquence des différentes suppressions et contractions effectuées à chaque niveau est conservée en mémoire.
brins liaisons marque α0 α1 α2 1 2 4 1 2 1 5 2 S01
Figure 5.11: Représentation implicite de la pyramide de la Fig. 5.8. Le tableau associé présente les images par α0, α1 et α2 des brins 1 et 2 au niveau initial de la pyramide.
Ainsi, cette représentation se compose d’une unique G-carte correspondant au niveau initial de la pyramide (cf. exemple Fig. 5.11), et trois marques sont associées à chaque brin lorsque celui-ci disparaît à un niveau. De même que pour les deux premières représentations, une marque indique l’opération ayant entraîné la disparition de la cellule incidente à ce brin, et une deuxième indique la dimension de cette cellule. Une troisième marque indique le niveau auquel cette opération est appliquée. Nous pouvons remarquer que ce système de marquage ne laisse aucune ambiguïté, puisqu’une cellule ne peut disparaître qu’une seule fois, et n’est donc marquée qu’une fois au plus.
Ce type de représentation est intéressant pour stocker une pyramide de manière compacte. C’est une généralisation nD de la représentation proposée en 2D dans [BK03a, BK06].
Dans [Sim06], nous avons prouvé que ces trois représentations étaient équivalentes, et nous avons effectué une étude de complexité (mémoire et temporelle) comparative mettant en avant les avantages et inconvénients de chacune d’elle.
Dans ce chapitre nous avons présenté la définition des pyramides généralisées, en donnant leurs principales propriétés, et en définissant les notions importantes de chemin de connexion et d’orbite généralisée. Ces deux notions permettent en effet de faire le lien entre les différents niveaux de la pyramide. Nous avons également défini trois représentations possibles de ces pyramides qui sont plus ou moins compactes en mémoire. L’intérêt de ces pyramides est de représenter différentes subdivisions d’un même objet, et d’autoriser la navigation entre ces subdivisions au travers des cellules et de leurs raffinements. De plus, nous profitons des définitions formelles des cartes et des opérations de contraction et de suppression afin de garantir la validité de la structure.
Ces pyramides généralisées se définissent à nouveau à partir des opérations de base (contraction/suppression) définies au chapitre 3. De ce fait, il est possible de transposer les définitions de la carte topologique présentée au chapitre précédent pour que les différents niveaux de simplification soient conservés au sein d’une pyramide. Il suffit pour cela que chaque niveau de simplification devienne un nouveau niveau dans la pyramide et plus une modification «sur place» de la carte du niveau précédent. Enfin, nous avons utilisé ici des cartes généralisées pour profiter de leur définition homogène en toute dimension, mais ce travail peut être porté de manière directe aux cartes combinatoires en utilisant les algorithmes de conversion présentés au chapitre 2. Il faut noter que ce travail a débuté dans [FB09b, FB09a] où les auteurs définissent les opérations de contraction et de suppression, et la notion de chemin de connexion pour les cartes combinatoires.
Dans [Sim06], nous avons également étudié d’autres aspects autour des pyramides non présentés dans ce chapitre. Nous avons tout d’abord défini des opérations de modification locale d’une pyramide. Le principe de ces opérations est de fournir une opération autorisant la modification du marquage des cellules d’un niveau de la pyramide : des cellules qui étaient supprimées ou contractées ne le sont plus, et à l’inverse des cellules qui survivaient deviennent marquées à supprimer ou à contracter. Ce type d’opération est intéressant car il autorise une modification locale de la pyramide, par exemple pour remettre en question la fusion de deux faces dans un niveau précis, sans avoir à recalculer entièrement la pyramide. La problématique sous-jacente est appelée le «relinking». Il faut en effet étudier l’impact de la modification locale sur les niveaux suivants de la pyramide. En effet, par exemple le fait de ne plus supprimer une cellule dans un niveau peut entraîner qu’une cellule qui était supprimée dans le niveau suivant ne soit plus supprimable. Nous avons proposé deux définitions de mise à jour d’une pyramide, qui dépendent de la manière dont les propagations sont effectuées, et nous avons prouvé que les pyramides obtenues après modification sont identiques à celles que nous aurions obtenues par construction (cf. [Sim06] pour le détail de ces opérations).
Plus récemment, nous avons commencé l’étude des pyramides dites «top-down». Le principe de ces pyramides est d’être défini de manière inverse par rapport aux pyramides présentées dans ce chapitre (qui sont appelées «bottom-up» afin de les différencier). Une pyramide top-down est donc la donnée d’une séquence de cartes, où chaque niveau est un raffinement du niveau précédent obtenue par l’application des opérations d’insertion et d’éclatement de cellules. Ce type de pyramide à l’avantage de mieux correspondre à un processus de construction par raffinement, où une zone d’intérêt d’un niveau est raffinée au niveau suivant. Nous avons utilisé ce type de pyramide dans un projet de traitement de segmentation de grandes images histologiques (de taille jusqu’à 320002 pixels), où l’utilisation de méthode bottom-up n’est pas envisageable. De plus, nous avons défini une notion de pyramide tuilée permettant de s’affranchir du problème lié à la taille des images. Nous avons ainsi pu proposer un modèle qui peut être chargé tuile par tuile en mémoire, les autres parties étant basculées sur disque (cf. [GBD09, GDB09, GBD10, GDB10] pour plus de détails).
Les perspectives de ce chapitre concernent principalement l’utilisation des pyramides et la définition d’opérations, ces deux problématiques étant fortement liées car le besoin d’opérations spécifiques apparaît souvent en lien avec des utilisations pratiques. Nous avons commencé à étudier l’utilisation des pyramides de cartes 2D et 3D dans le but de proposer des méthodes de segmentation multi-échelle (qui seront évoquées au chapitre 7) mais ces travaux doivent être poursuivis afin de valider les apports de ces structures pour la résolution de problématiques précises. Nous souhaitons pour cela approfondir les travaux autour des problématiques liées à l’image, dans des méthodes de segmentation ou de reconnaissance. L’idée est d’utiliser une pyramide représentant un même objet à différentes échelles, puis de combiner les résultats des différentes échelles pour proposer des méthodes plus précises mais aussi plus rapides. En effet, en montant dans les niveaux supérieurs de la pyramide, le nombre d’éléments diminue et donc les temps de traitement également.
Nous souhaitons pour cela nous intéresser à la définition d’opérations spécifiques et à la manière dont elles utilisent les différents niveaux de la pyramide, afin d’être améliorées. Nous souhaitons également étudier l’utilisation des pyramides en modélisation géométrique, où nous envisageons de définir des opérations de modélisation multi-échelles, là encore en s’appuyant sur les liens entre les cellules des différents niveaux. Une nouvelle fois, nos définitions génériques nD montrent leur avantages en autorisant différentes applications en différentes dimensions. Une dernière perspective de recherche concerne la possibilité de compacter plusieurs niveaux d’une pyramide en un seul. L’objectif est ici de diminuer l’espace mémoire nécessaire à la représentation d’une pyramide, mais également les temps de parcours puisqu’il y aura moins de niveaux différents à traverser. Nous souhaitons pour cela étudier des méta-opérations regroupant différentes suppressions et contractions, en autorisant les cellules à ne plus être disjointes, tout en garantissant l’absence de perte d’information.
Nous allons maintenant présenter des opérations de calcul d’invariants topologiques sur les cartes. L’objectif de ce chapitre est de fournir ces opérations afin de pouvoir par la suite s’en servir pour caractériser les objets, ou encore pour guider ou contrôler des opérations.


