Laurent Feuilloley, Michel Habib.
SIAM Journal of Discrete Mathematics (SIDMA). 2021.
doi:10.1137/19M1280399
Abstract
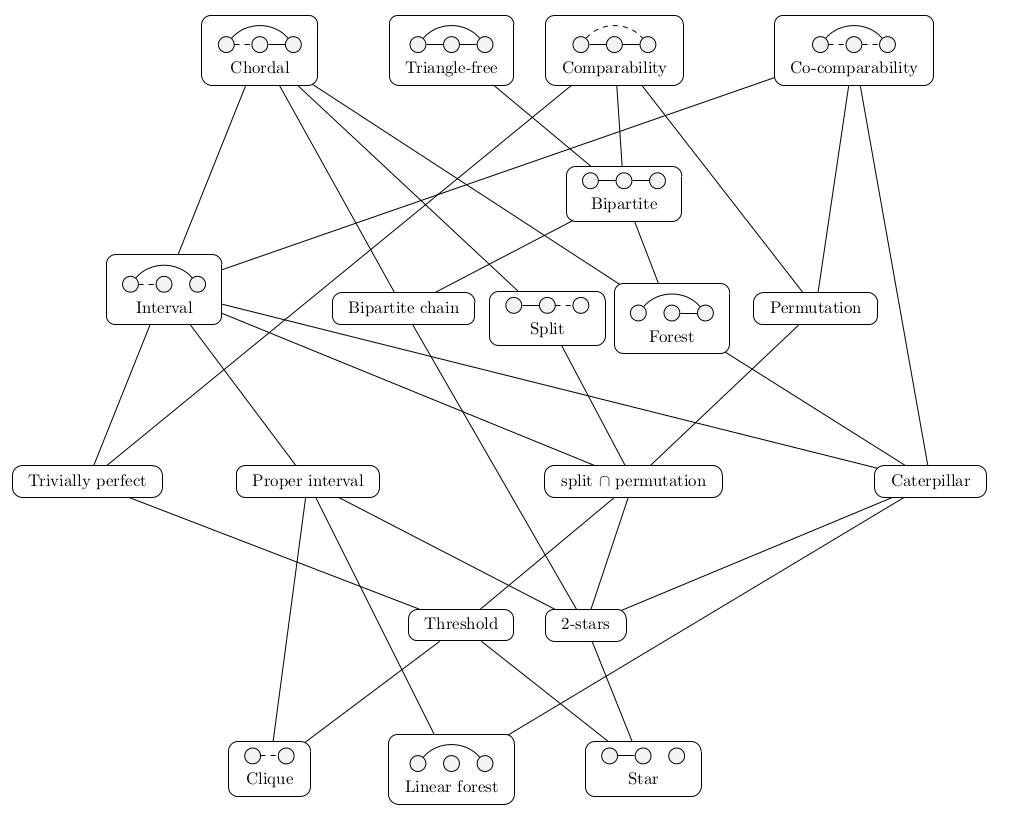
This paper deals with the characterization and the recognition of graph classes. A popular way to characterize a graph class is to list a minimal set of forbidden induced subgraphs. Unfortunately, this strategy hardly ever leads to a very efficient recognition algorithm. On the other hand, many graph classes can be efficiently recognized by techniques that use some ordering of the nodes, such as the one given by a traversal.
We study specifically graphs that have an ordering avoiding some ordered structures. More precisely, we consider structures that we call \emph{patterns on three nodes}, and the complexity of recognizing the classes associated with such patterns. In this domain, there are three key previous works. Independently Skrien (1982) and Damashke (1990) noted that several graph classes such as chordal, bipartite, interval and comparability graphs have a characterization in terms of forbidden patterns. On the algorithmic side, Hell, Mohar and Rafiey (2014) proved that any class defined by a set of forbidden patterns on three nodes can be recognized in time $O(n^3)$, using an algorithm based on an extension of 2-SAT. We improve on these two lines of works, by characterizing systematically all the classes defined by sets of forbidden patterns (on three nodes), and proving that among the 22 different classes (up to complement) that we find, 20 can actually be recognized in linear time.
Beyond these results, we consider that this type of is very useful from an algorithmic perspective, leads to a rich structure of classes, and generates many algorithmic and structural open questions worth investigating.